円周角の意味や計算方法などの基本がどのようなものか気になるかもしれません。円の性質のひとつとして中学で出てきますが、円周角の関係性や証明の仕方は押さえておきたいですよね。円周角の定理は中学だけでなく受験でもよく出てくる内容であり、数学の円の性質の問題にも関連があるため使い方をしっかり理解するのが大切です。今回は、円と角度の定理である、円周角の利用や角度の求め方、円周角の定理の逆とはがどのようなものかについてご紹介します。
◎数学の円における定理、円周角の性質や公式は?
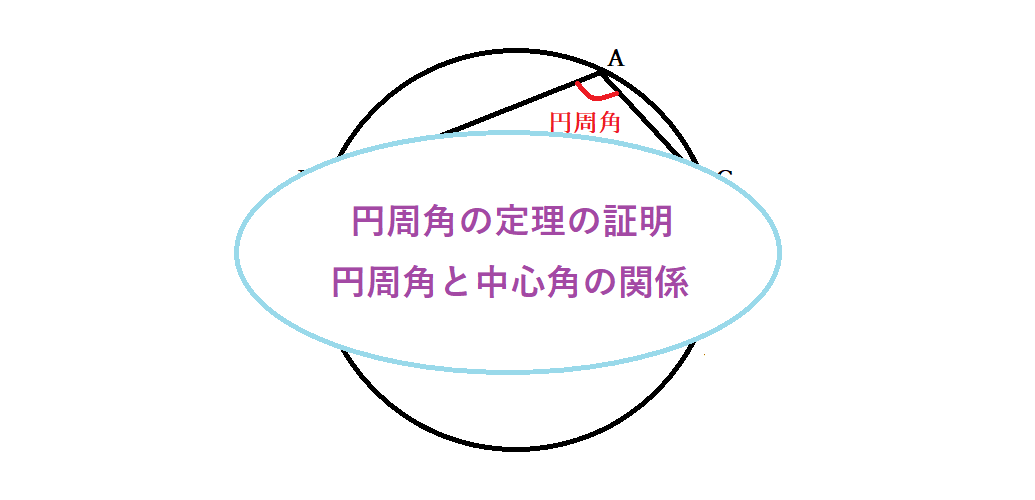
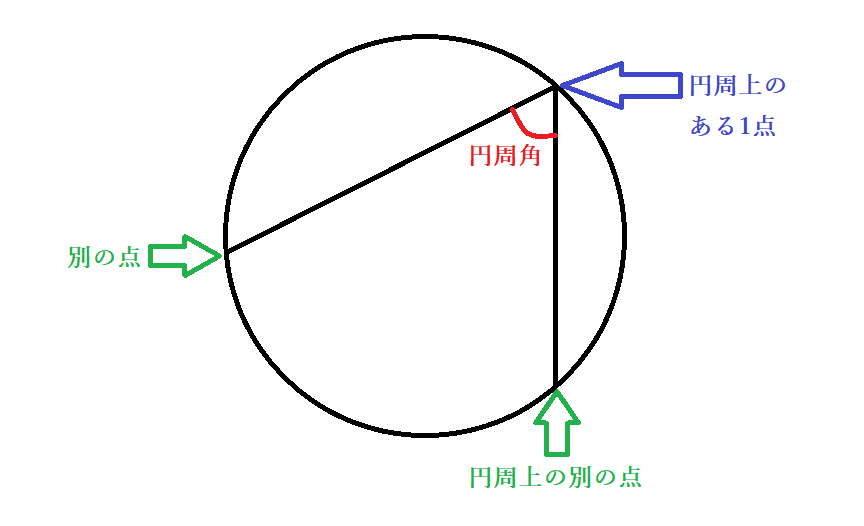
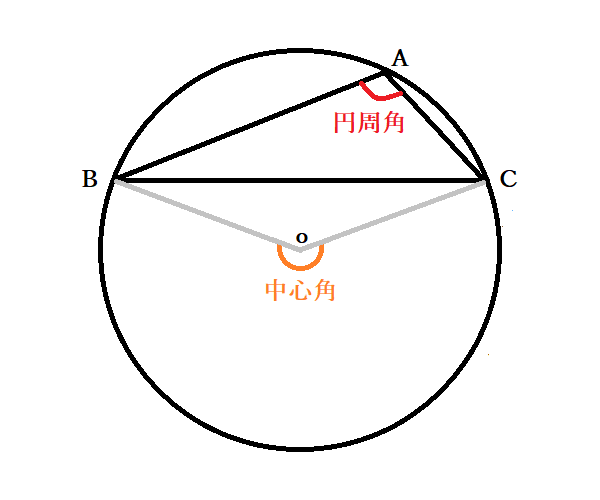
中学数学ででてくる円周角とは、円の上にある1点から円の上にある別の2点を結ぶ2つの線分が作る角のことです。イメージが難しい場合は、図で確認するとよいでしょう。赤い色を塗った部分を円周角と言います。
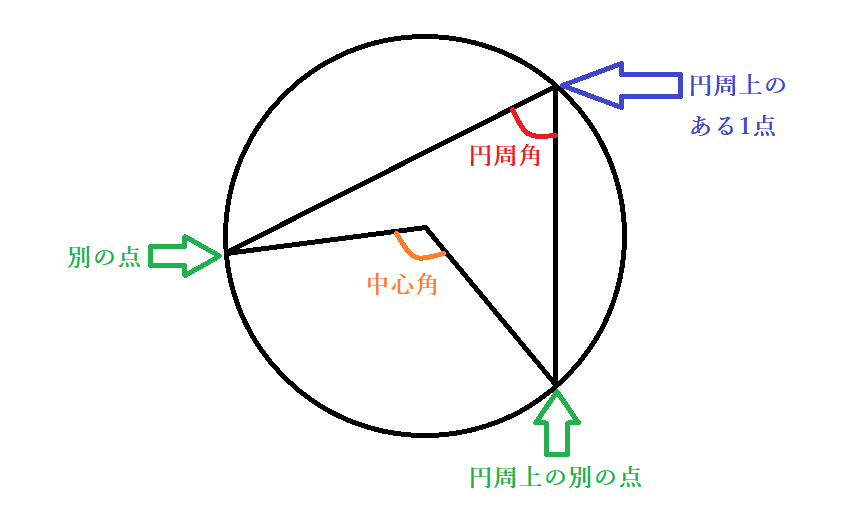
先ほどの『別の2点』からそれぞれ、円の中心にも線を引いてみましょう。円周上の2点と中心を結んだときにできる角が中心角です。数学の円の性質として、円周角は中心角の半分の大きさに必ずなります。円の角度の定理として、円周角の定理と呼び、円の上にあるどの3点においても成立するのが特長です。円周角の公式としては、円周角=中心角÷2が使われ、数学における円周角の問題でよく出てきます。
◎中3数学でよくある円周角の問題の例
中3数学でよくある円周角の問題の例で代表的なのは、同じ弧に対する円周角は等しいことを利用して、複数の角の大きさを順に求めていく問題です。また、直径に対する円周角は常に90度になることを利用するタイプもよく出題されます。円周角の解き方には「弧が等しければ角度も等しい」ことを利用する場合もあり、円周角の性質や意味を理解しているかだけでなく、図の読み取り力や補助線を引く力もポイントです。
◎円周角の定理の証明問題:円周角と中心角にまつわる問題
円周角の公式は、すぐにはイメージしづらいかもしれません。円周角の定理の証明問題で実際に出題される事例として、円周角と中心角にまつわる問題を通してなぜ成り立つのかをみていきましょう。ここでは『円の上にある点』をA・『別の2点』をB.C・中心をOとします。3点ABCを結んだとき、三角形と円の位置関係で考えられるのは次の3種類です。
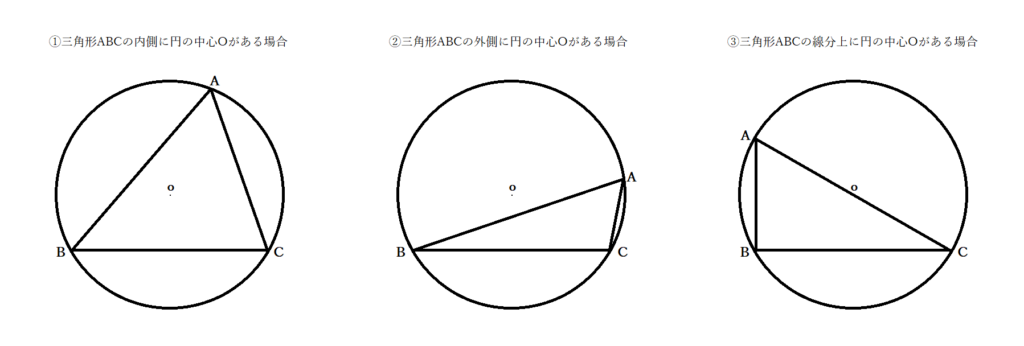
①三角形ABCの内側に円の中心Oがある場合
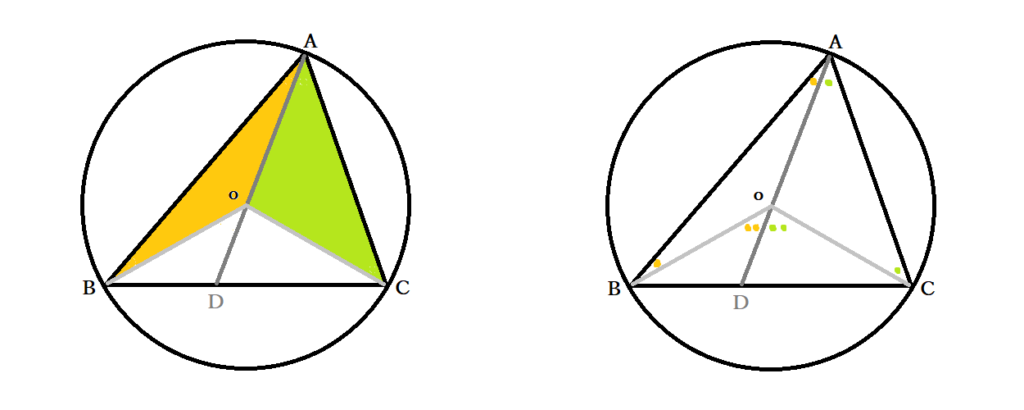
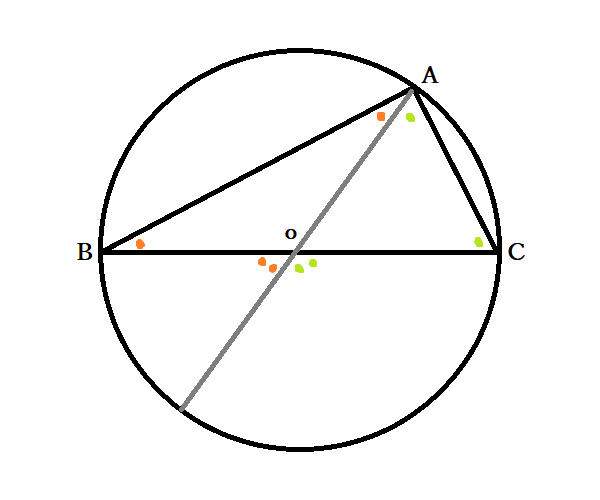
AOを結び、延長とBCの交点をDとします。これにより三角形ABCは△ABDと△ACDに分かれました。△OABは、OA=OB=半径より二等辺三角形で、∠OAB=∠OBA=橙色の●です。同様に三角形OACは、OA=OC=半径より∠OAC=∠OCA(=黄緑色の○)が成立します。三角形の外角の定理より、∠DOB=∠OAB+∠OBA=●●・∠DOC=∠OAC+∠OCA=○○です。よって円周角∠Aは∠BAC=∠OAB+∠OAC=●+○、中心角は∠BOC=∠DOB+∠DOC=●●+○○で、成り立つことが証明できました。
②三角形ABCの外側に円の中心Oがある場合
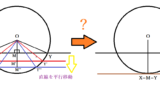
AOの延長と円周との交点をDとします。△OABはOA=OB=半径で二等辺三角形なので∠OAB=∠OBA=橙色の●、同様に△OACは∠OAC=∠OCA(=黄緑色の○)です。外角の関係性から、∠DOB=∠OAB+∠OBA=●●・ ∠DOC=∠OAC+∠OCA=○○となり、無事に示せました。
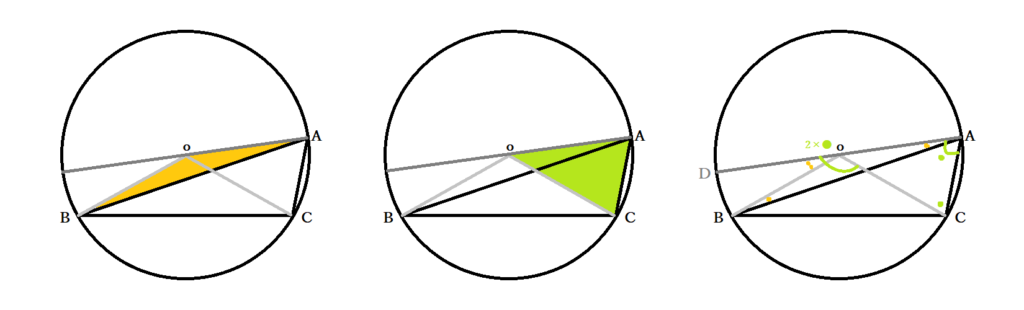
ちなみに、∠Aが90度以上つまり鈍角の場合は中心角は180度以上になります。同じように証明できますので、気になる場合は確かめてみましょう。
③三角形ABCの線分上に円の中心Oがある場合
さらに2通り考えられます。Aが入っている線の上つまりABまたはAC上にOがある場合と、『別の2点』BCのどこかに円の中心がある場合です。
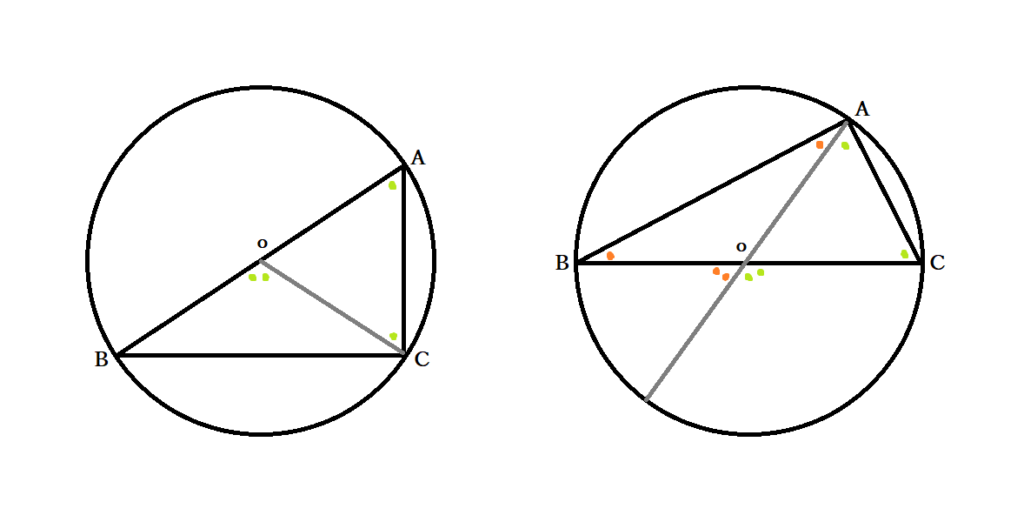
線分ABまたはAC上に円の中心がある場合
BとCは対称のため、ここでは線分AB上にOがある場合のみを考えましょう。OCを結ぶと、OC=OAより∠OCA=∠OAC(=黄緑○)が成り立ちます。外角の関係から、∠BOC=∠OCA+∠OAC=○○です。
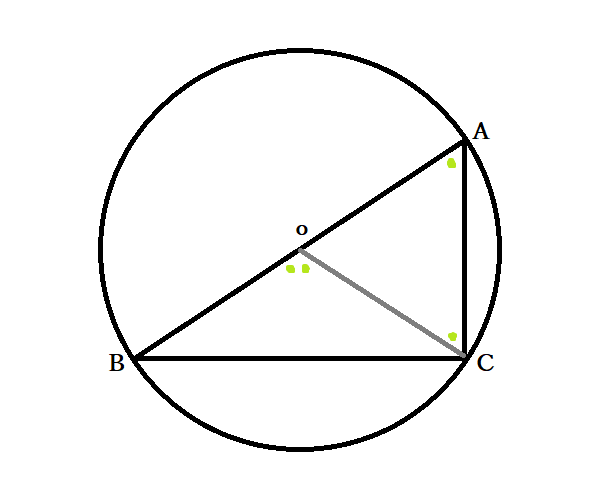
線分BC上に円の中心がある場合
AOの延長とBCの交点をDとすると、①と同様の関係が成り立ちます。BC上にOがあるとき、B・C・Oは一直線上なので∠BOC=180度です。よって円周角∠A=90度となり、中心を通る辺に対する円周角は直角になることが示せました。
◎[中学数学]円周角の練習問題で計算と角度の求め方をおさらいしよう
円周角の練習問題は角度の求め方や基本的な計算を定着させるのにとても効果的です。中学数学ででてくる円周角の練習問題では、「同じ弧に対する円周角は等しい」「中心角の半分が円周角になる」といった基本の性質がよく使われます。こうした問題では、円周角の関係性と図の中で与えられた角度をヒントにして、求めたい角度を順に導く力が必要です。円周角の問題の応用として、補助線を引いて三角形を分割し、複数の角の和や差を求めるというのもよくあるパターンに挙げられます。
◎円周角の定理の逆とは?問題の事例(中学や受験でもよく出る)
円周角の定理の逆とは、「同じ円周角が成り立つ場合、その点は円周上にある」ことです。円周角の定理における中学や受験の問題としてもよく出題され、ある点が本当に円周上にあるかを角度の情報から判断する必要があります。例として、三角形のある角が90度であれば、その三角形は直径を弦とする円に内接することが証明できます。
◎円周角の問題の応用:円周角の利用で導ける内接四角形
円周角の応用例としては、四角形が出てくることもあります。頻出なのは、内角のいずれかがわかっていて、対角を求める問題です。「内接する四角形の向かい合う角の和は180度」が成り立つ理由が気になるかもしれません。この性質も円周角の利用で説明できます。
ここでは、点Oが中心の円に内接する四角形ABDCを作りましょう(∠Aの対角が∠D)。OA=OB=OC=OD(半径)より、∠OAB=∠OBA=赤●・∠OBD=∠ODB=緑●・∠ODC=∠OCD=黄●・∠OCA=∠OAC=青●が成り立ちます。∠A=∠OAB+∠OAC=赤●+青●・∠D=∠ODB+∠ODC=緑●+黄●なので、∠A+∠Dは4つの角度の合計です。一方で、四角形の和は360度であることから∠A+∠B+∠C+∠D= ∠OAB+∠OAC+∠OBD+∠OBA+∠ODB+∠ODC+∠OCA+∠OCD=(赤●+青●+ 緑●+黄●)×2=360度が成り立ちます。よって、内接する四角形の向かい合う角度の和は180度だと証明できました。
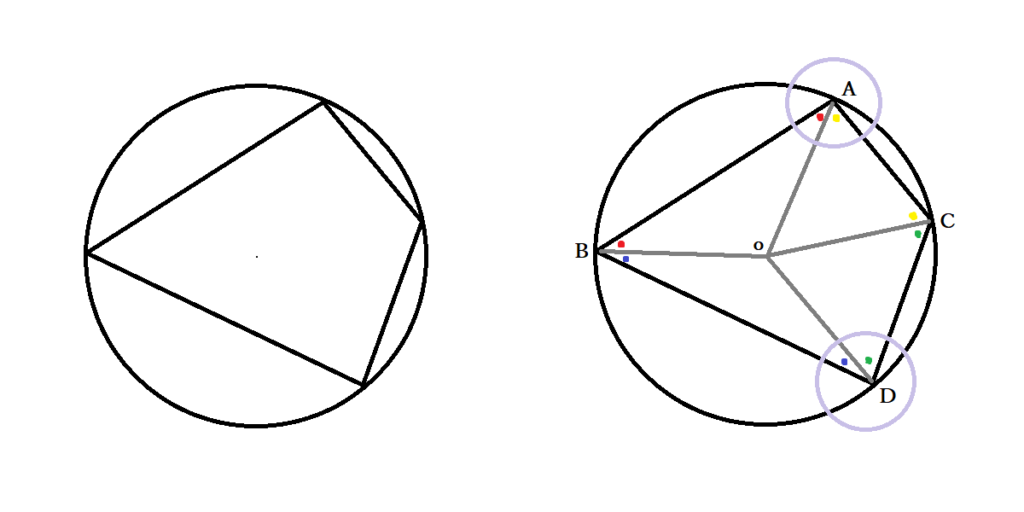
中心角と円周角の関係を利用すると、∠COB(∠A側)+∠COB(∠D側)=2×∠D+2×∠A=2×(緑●+黄●+赤●+青●)が1周の360度です。つまり∠A+∠D=赤●+ 青●+ 緑●+ 黄●=180度で同様に示せます。
◎まとめ
今回は、数学の円における定理である、円周角や証明の仕方、内接四角形への応用などについてご紹介しました。円の性質として中学でも頻出の問題であり、定期テストや高校入試に向けて確実に理解しておきたい内容です。中心角との関係や、問題のパターンを押さえることで、角度の求め方や計算がスムーズになります。また、応用問題では図形の読み取り力や性質の活用が重要になるため、繰り返し練習しながら身につけていきましょう。最後までお読みいただきありがとうございました。