◎円の接線の角度は本当に90度(直交)なのか?
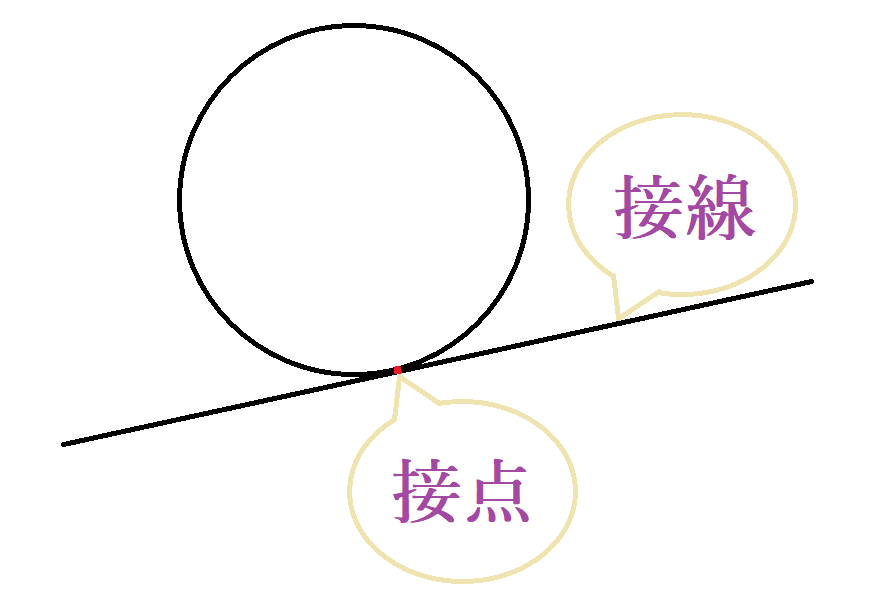
円の接線は、円と直線が1点で交わるときの直線を指します。中学数学ではごく自然に使われる言葉ですが、「円の接線が90度なのはなぜ?」と思ったことがあるかもしれません。教科書や解説では、「円と接線は直交する」と当然のように扱われます。しかし、その説明をよく読むと、図のイメージに強く依存していたり、限りなく近づけるといった直感的な表現で済まされていることも少なくありません。円の接線が垂直になぜなるのかは、あまり知られていない断言できる方法があるのが特徴です。今回は、円の接線の角度が90°になることの理由を、中学数学の範囲で考えられる3つの視点でご紹介します。
◎円の接線が90度になることの証明①:直線を平行移動して考える
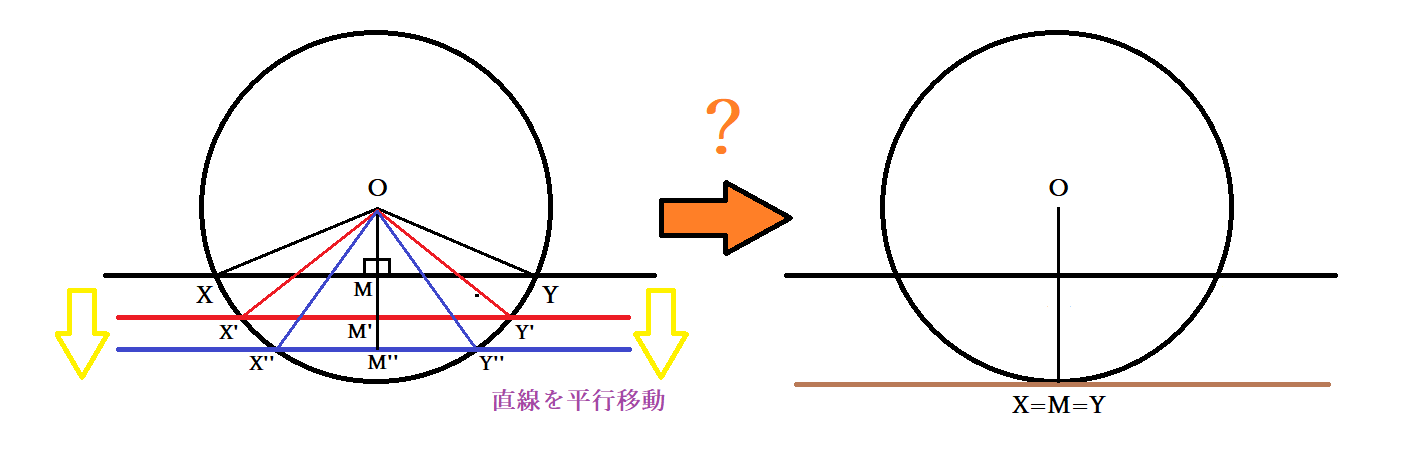
円の接線が直角になる証明について、まずは多くの教科書や解説で紹介されている代表的な考え方から確認しましょう。円と2点で交わる直線を考え、円の中心をO、交点をX・Yとします。このとき、線分XYの中点をMとすると、三角形OXMとOYMについて、OMは共通、XM=YM(中点)、OX=OY(半径)で三辺がそれぞれ等しく、これらの三角形は合同です。合同な三角形では対応する角も等しいため、∠OMX=∠OMYが成り立ちます。また、X・M・Yは一直線上にあるので、∠XMY=180°です。したがって∠OMX=∠OMY=90°となり、OMは直線XYと直角に交わることがわかります。
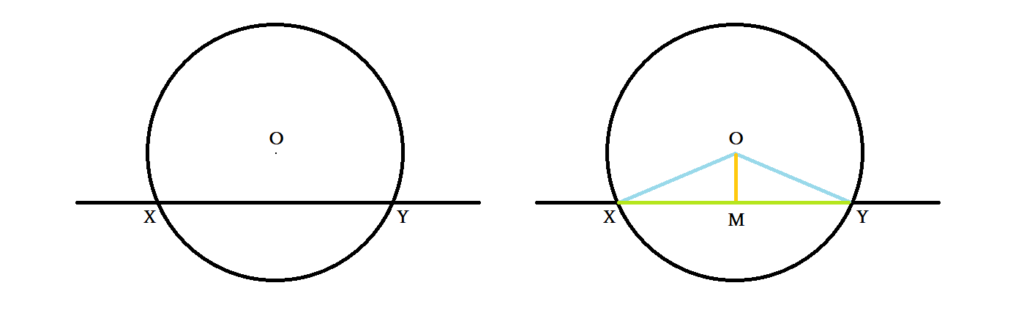
ここで、直線XYを円の内部で少しずつ平行に動かし、XとYの距離が短くなるようにしてみましょう。この操作を行っても、三角形の合同関係や直角の関係は変わりません。そして最終的に、XとYが一致する位置では、直線は円と1点で交わり、接線になります。このときも先ほどと同じ関係が保たれているため、接点でも90度というわけです。

●この証明で「本当に90度だと言い切れるのか?」
ここまでの説明は、円の接線が90°であることの証明として非常によく使われています。しかし、「本当にこれで十分なのか?」と疑問に感じる方もいるかもしれません。直線を動かしていく過程で、2点で交わる場合から1点で交わる場合へと移っていますが、その瞬間にも角度が必ず90度のまま保たれると、厳密に言えるでしょうか。

イメージとしては、確かに直角のまま近づいていきそうに見えます。しかし、数学では「そう見える」「なめらかに変化するはずだ」という感覚だけで結論を出すことはできません。もし厳密に扱うなら、限りなく近づけるといった操作には極限の考え方が関わり、高校数学の内容が必要になります。つまり、この①の方法は直感的には非常に分かりやすいものの、中学数学としては【説明】にとどまっており、完全に証明し切れているかは慎重に考える必要があるのです。そこで次に、別の視点から本当に90度でなければならないことを確かめていきます。
◎円の接線が直角であることの証明②:90度以外だと仮定した背理法
次は背理法を使って考えます。背理法とは、ある仮定を置くと矛盾が生じることを示し、その仮定が誤りである(つまり相反する内容が正しいもの)と結論づける方法です。
円と直線がPで接しているときの角度が90度ではないと仮定しましょう。円の中心Oから直線に垂線をおろし、その足をQとします。垂線である以上、∠OQP=90°で、PとQは異なる点です。ここで、Qを中点となるようにPの反対側に点Rを取ります。
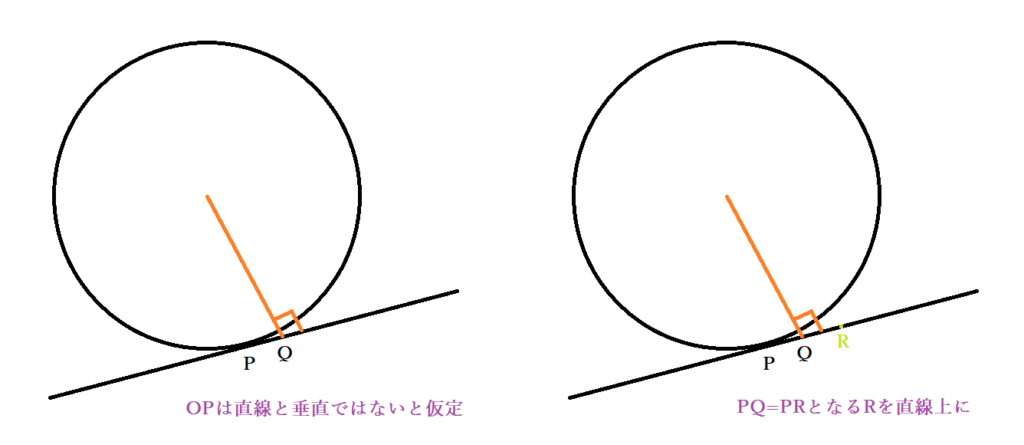
△OPQと△ORQにおいて、OQは共通、PQ=RQ、そして直線⊥OQから∠OQP=∠OQR=90°です。よって、2辺とその間の角が等しく、これらの三角形は合同になります。合同である以上、OP=ORが成り立ち、Pは円周上の点なので、OPは半径です。すると、円の中心Oから長さの等しいRもまた円周上にあります。つまり、直線はPとRの2点で円と交わることになり、「接線は円と1点のみで交わる」接線の条件を満たしません。この矛盾から、仮定が誤りであることが分かり、円の接線の角度が90°であることが結論づけられます。

◎円の接線が垂直になることの証明③:辺の長さと角の大小関係に注目する
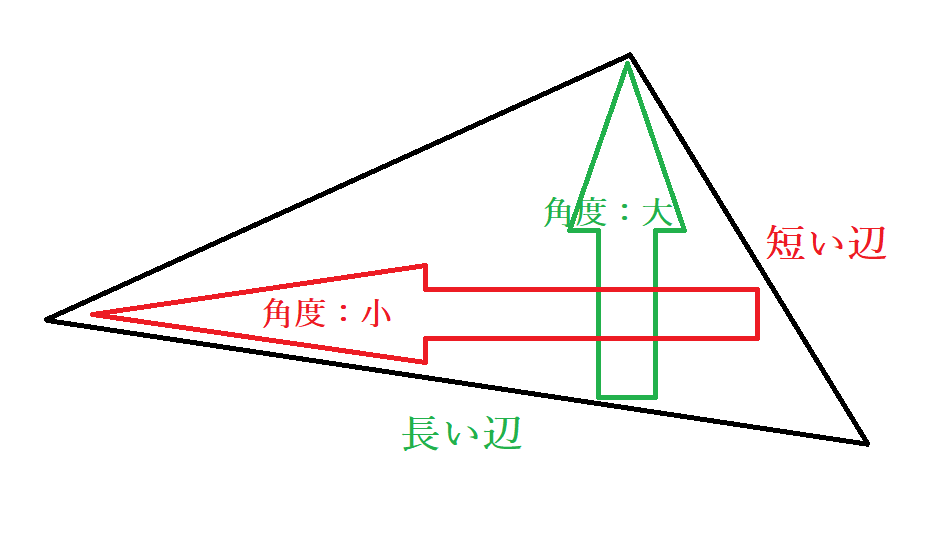
円の接線が90度になることのもう一つの証明方法は、辺の長さと角の大きさの大小関係を利用するものです。三角形で、長い辺の対角は短い辺の対角よりも大きい性質があり、逆も成立します。
円と直線の接点をXとし、接線が垂直ではないと仮定します。円と接線は交点が1つだけなのが条件ですから、Xのほかにはありません。その場合、円の中心Oから接線へ90度になるように垂線を下ろすとその足YとXは別の点です。
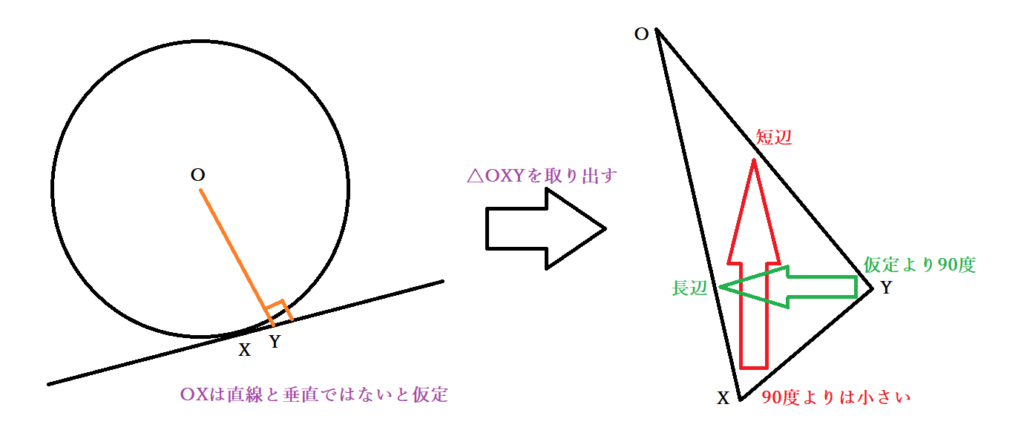
三角形OXYを考えると、∠OYX=90°です。このとき、直角に対する辺OXは斜辺ではありませんから、∠OXYは90度より小さくなります。したがって、角の大小関係からOX>OYが成り立つはずです。しかし、Yは円の外部にあるため、中心Oからの距離OYは半径OXより長くなります。つまりOX<OYとなり、先ほどの結論と辻褄が合いません。この矛盾から、仮定が誤りであると分かり、円の接線が垂直であることが証明されました。
◎接弦定理を利用した証明ができない理由
接弦定理は、円と直線が接するときに、弦のなす角と円周角との関係性を示した定理です。直径を通るときに、円周角が90度になることから接弦定理によって円と接線が直交することが求められるでしょう。

しかし、接弦定理そのものの証明では、円と直線が接点で90度に交わるを前提として使っています。そのため、接弦定理を用いて証明しようとすると、前提と結論が入れ替わった循環的な議論になってしまうのです。これは、いわゆる「卵が先か鶏が先か」の問題と同じ構造となります。

数学では、証明に用いる事実は、すでに成り立っているものとして扱わなければなりません。本記事では、円の接線が90°であることを基礎として接弦定理が成り立つ流れを採用しているため、逆向きの証明については扱いません。接弦定理そのものについては、別記事で詳しく解説してますので、あわせて参考にしていただければ幸いです。
◎まとめ
今回は、「円の接線が垂直(90度)になるのはなぜ」なのかについて、中学数学の範囲で考えられる3つの視点でご紹介しました。接点が90度であることは、図を見ると当然のように思えますが、その説明の仕方によっては直感に頼りすぎてしまうこともあります。本記事では、平行移動による説明を出発点としつつ、背理法や角と辺の大小関係を用いて、多角的に検証しました。一つの説明だけで納得するのではなく、「本当にそう言い切れるのか?」と立ち止まって考えることでより確かな理解につながるでしょう。最後までお読みいただきありがとうございました。
関連記事