数学では角の二等分線や内心を使った問題を見たことがあるかもしれません。数学における内心とは何かがわかると三角形の性質もより深く知ることができますよね。今回は、内接の意味やコンパスを使った二等分線の作図、角の2等分線の定理の証明など関連する内容を含めてご紹介します。
◎内心とは・多角形とは簡単に解説、内接の意味も
内心とは簡単にいうと、三角形など多角形に内接する円の中心を指します。多角形や内接の意味もみていきましょう。
●多角形とは簡単に、読み方・一覧・定義で小学生で習うのは?
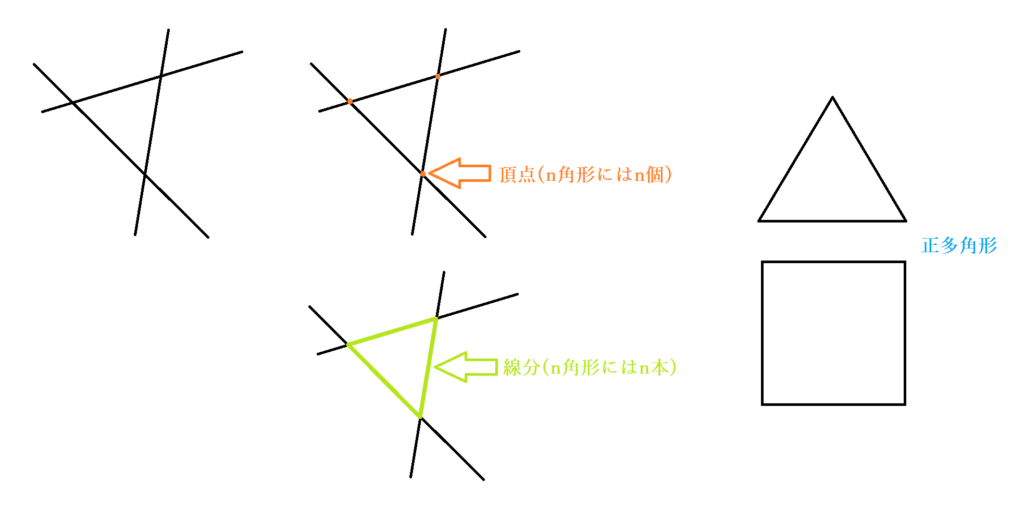
多角形とは簡単にいうと、3つ以上の直線で囲まれた部分をつないでできるものです。多角形の読み方は「たかくけい」であり、N角形はいずれも当てはまるため、一覧では表すことができません。正多角形の立体だけでも正三角形・正方形・正五角形・正六角形…などがあります。多角形の定義で小学生でも習うのが角度に関するものです。多角形の内角の和はN角形:(N-2)×180度であるのに対し、多角形の外角の和は360度と一定の値になります。
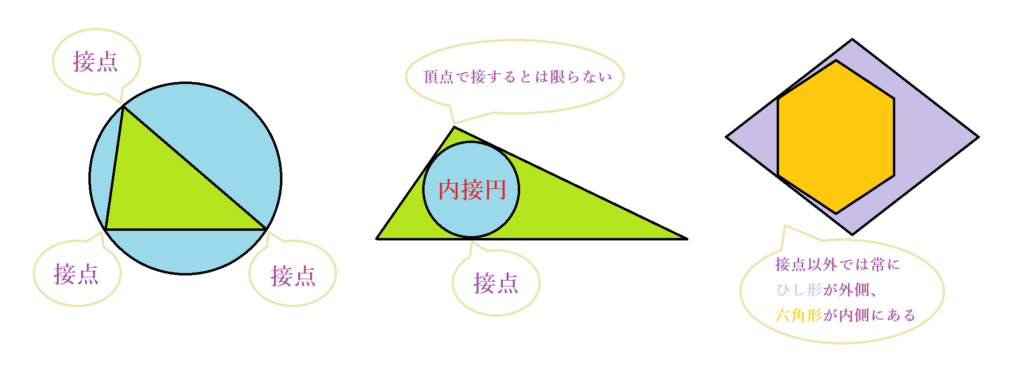
●内接の意味・内接円とは?
内接が意味するのは、二つの図形の関係性です。片方の図形の頂点または辺のどこかがもう片方の図形の頂点または辺のどこかと一致し、かつそのほかの点は全てもう片方の図形の内側にある状態を指します。例として、左にあるのは三角形が円に内接している様子です。三つの頂点が円周上と一致し、残りの辺の部分は全て円の内側にありますよね。特に、内側にあるものが円の場合はそれを内接円と呼びます。
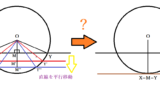
円同士の場合は少し特殊で、円周上の1点のみ同士が接してかつそれ以外の点では片方の円がもう片方の円よりも内側に位置しています。1点のみなのは、楕円でない場合には形が同じで、2点以上共有するのは完全一致以外は考えられないからです。

◎三角形の内接円の書き方、三角形の角の二等分線の作図をコンパスで
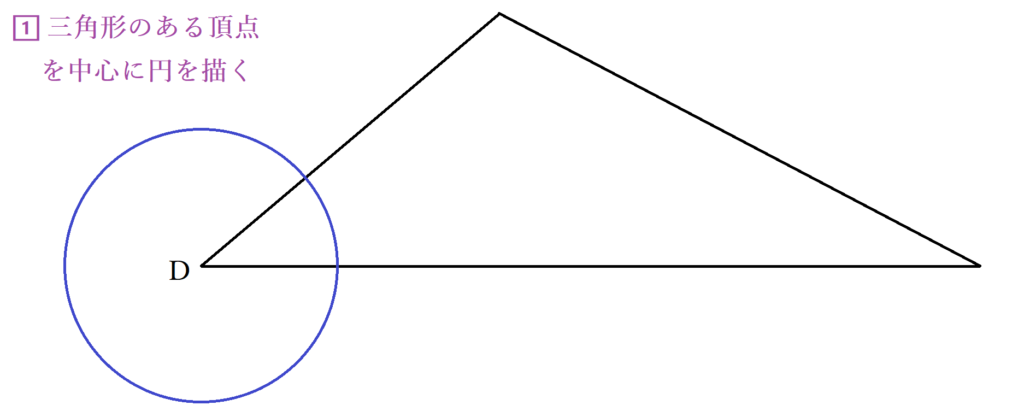
三角形の内接円の書き方が気になるかもしれません。内接円は中心が見つかればあとは三角形に接するように書ければ良いので、円の中心を探すのがポイントです。そこでまずは、三角形の角の二等分線をかいていきます。角の二等分線の作図はコンパスを用意しておきましょう。例では、頂点Dを中心にコンパスで円を描き、三角形の辺との交点をP.Qとします。
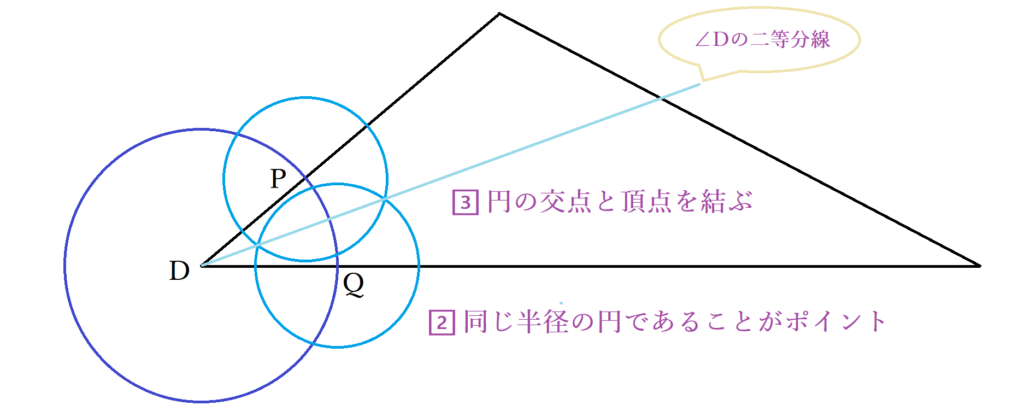
P.Qを中心に同じ大きさの円を描き、その二つの円の交点をRとしましょう。直線DRは∠Dの二等分線になります。PQはDを中心とする円周上にあるためPD=QD、RはP.Qから距離の等しい点としているのでPR=QR、DR共通で△PDRと△QDRは合同になるためです。
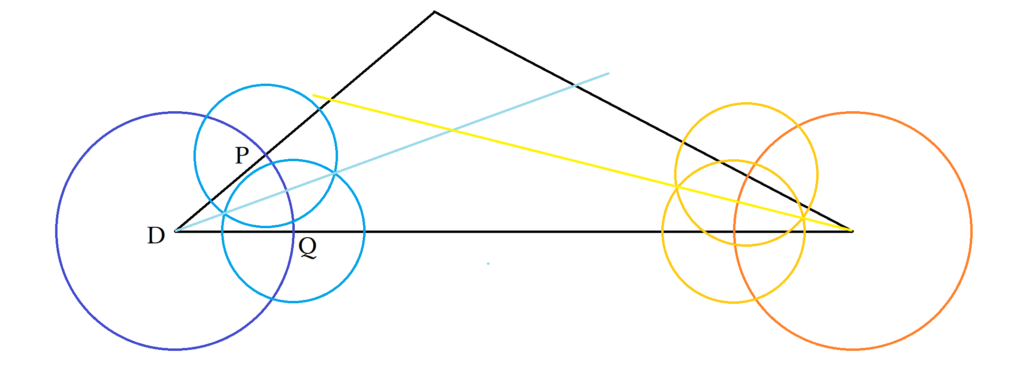
同じ流れで、別の頂点から二等分線を引き、交点をIとしましょう。
接するように円を描くためには、接点を求める必要があります。Iを中心に円を描き、三角形の1辺との2つの交点をS.Tとしましょう。S.Tを中心に円を描き、その二つの円の交点をUとしてIとUを結べば、垂線になるため交点Vが内接円と三角形の辺の接点だとわかります。Iを中心とし、IVが半径になるように円を描くと、三角形の内接円の作図が完成です。ここでの円の中心Iのことを内心と呼びます。
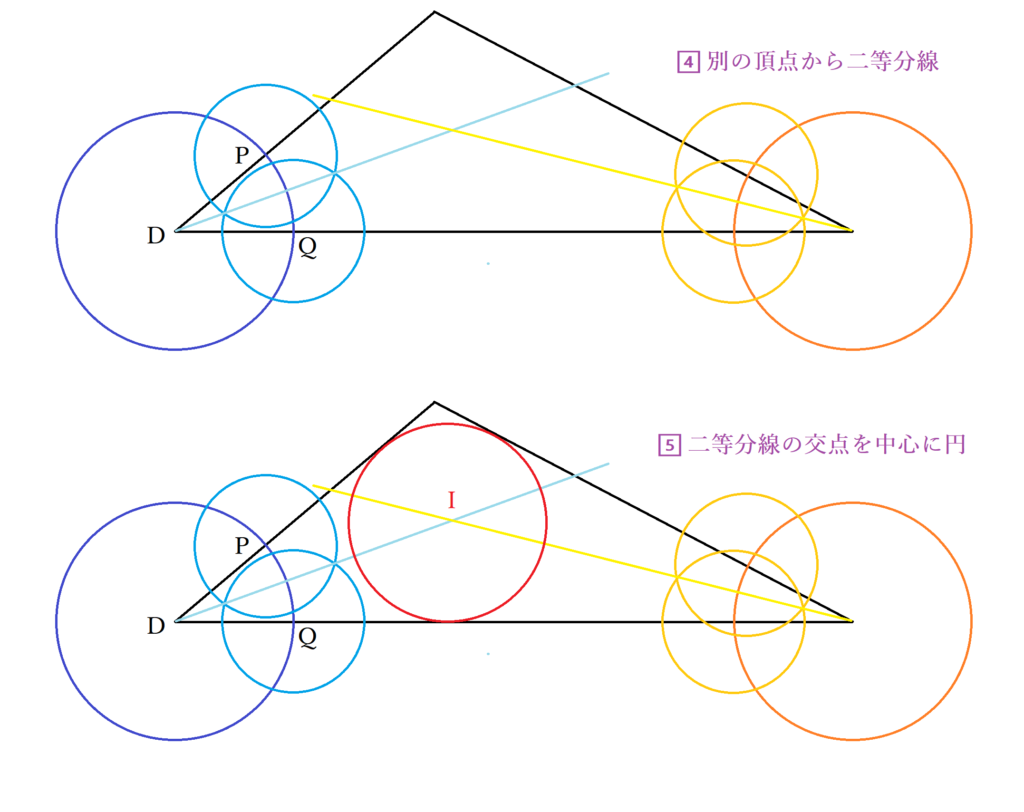
◎内心と角の二等分線の性質(中学の問題)なぜ一点で交わる?
角の二等分線の性質として中学でも出てくるのが、三角形の二等分線が1点で交わるというものです。数学の角の二等分線の定理は中学の問題でも証明や計算で出されますから、どのような仕組みなのかは知っておきたいかもしれません。内心つまり角の二等分線の交点がなぜ1つに定まるのかをみていきましょう。DEFにおいて、∠Dの二等分線と∠Eの二等分線の交点をIとします。Iから辺EF.DF.DEへの垂線をそれぞれX.Y.Zと表してみましょう。
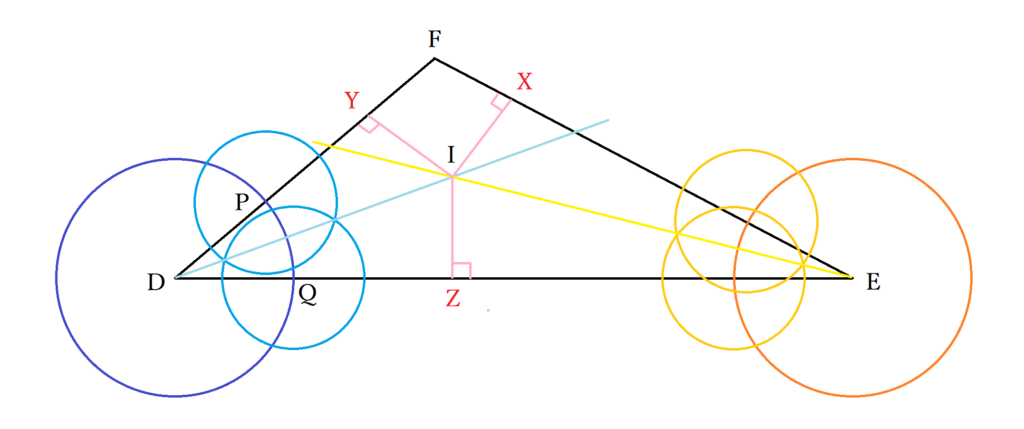
△DIYと△DIZにおいてIDは共通・∠IDY=∠IDZ(∵IDは∠Dの二等分線)・Iから辺DF.DEへの垂線をそれぞれY.Z としているので、∠DYI=∠DZI=90度です。つまり、△DIYと△DIZは斜辺と他の1つの角が等しい直角三角形のため合同であり(△DIY≡△DIZ)、IY=IZが成り立ちます。
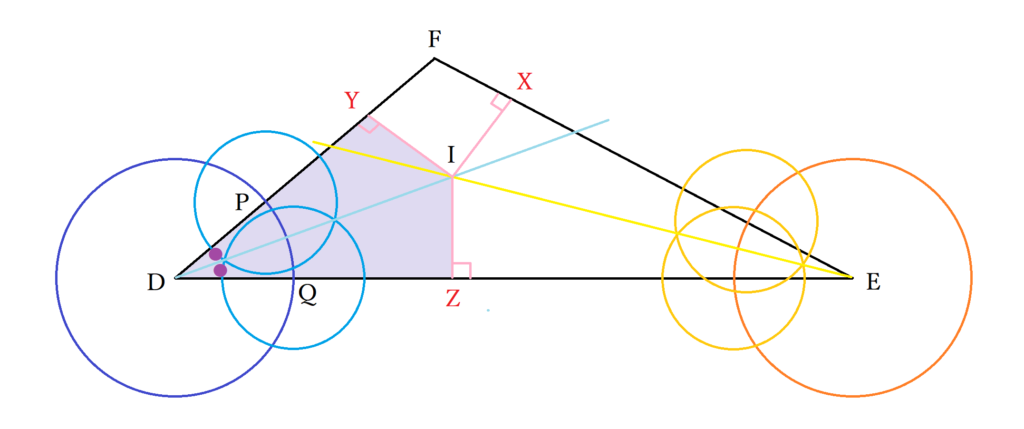
同様に、△EIZと△EIXにおいてIEは共通・∠IEZ=∠IEX(∵IEは∠Eの二等分線)・Iから辺DE.FEへの垂線をそれぞれZ.X としているので、∠EZI=∠EXI=90度です。つまり、△EIZと△EIXは斜辺と他の1つの角が等しい直角三角形のため合同であり(△EIZ≡△EIX)、IZ=IXが成り立ちます。したがって、IX=IY=IZとなり、Iを中心に三角形DEFの3つの辺に接する円が描けることがわかりました。
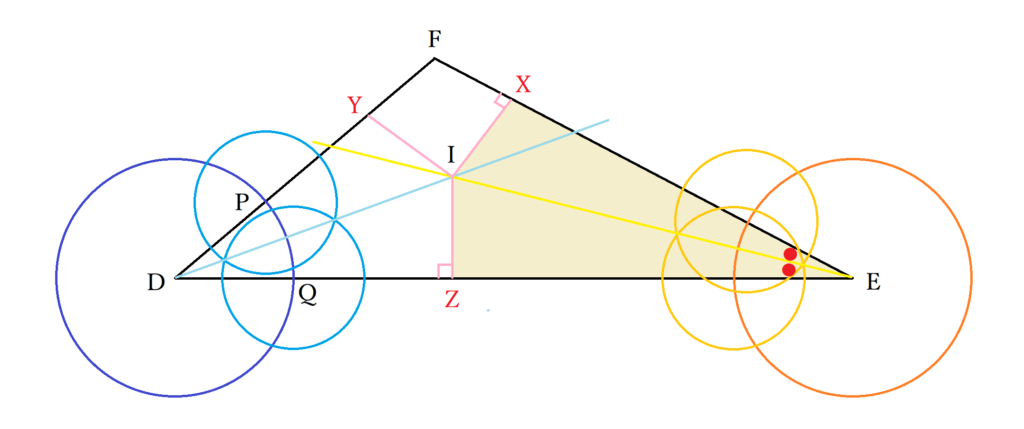
ここで、FからIに向けて線を引いてみましょう。△FIXと△FIYにおいてIFは共通・ 先ほどの結果からIX=IY・Iから辺FE.FDへの垂線をそれぞれX.Yとしているので、∠FXI=∠FYI=90度です。つまり、△FIXと△FIYは斜辺と他の1つの角が等しい直角三角形のため合同であり(△FIX≡△FIY)、∠IFX=IFYが成立します。これより、三角形の残りの一つの内角二等分線は、他の角の二等分線の交点を通ることがわかりました。
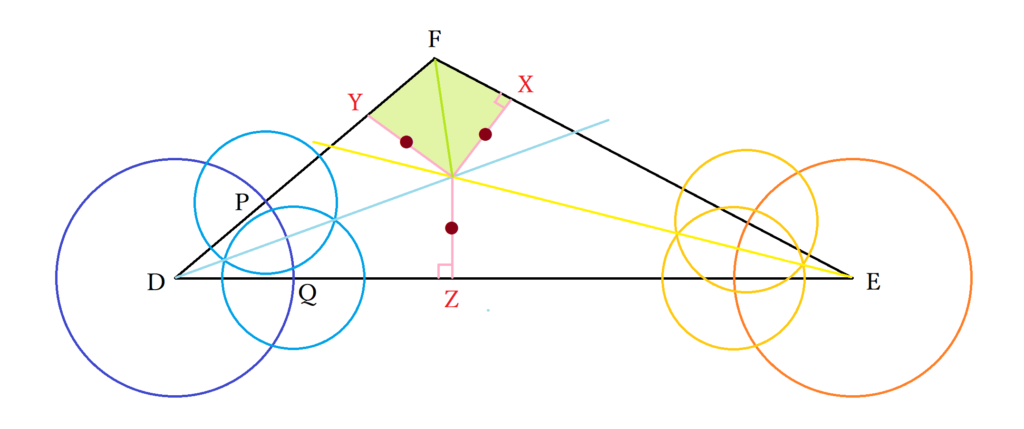
なお、ここでは円の接線が90度であることを利用しています。当たり前のように教わる内容かもしれませんが、その理由を考えると意外と奥が深いものです。なぜそうなるのかについては、こちらの記事で詳しくご紹介しています。
◎まとめ
今回は、数学では角の二等分線に関して、コンパスを使った二等分線の作図、角の2等分線の定理の証明などをご紹介しました。三角形における内接円の書き方は、角の二等分線をコンパスでつくることがポイントです。角の二等分線の定理は中学などで関連問題が多く出てきますので、なぜそうなるのかという深い部分で押さえておくようにしましょう。最後までお読みいただきありがとうございました。