三平方の定理とはどのようなものかわかりやすく知りたいかもしれません。三平方の定理の定義づけなどが簡単に押さえられているだけでも数学で図形を解く際の幅が拡がりそうですよね。三平方の定理は整数比や角度で計算ができるなど身の回りでも役立つ場面が多い公式です。今回は、中学数学で学ぶ直角三角形の三平方の定理をExcelの図(オートシェイプ)挿入を使いながらご紹介します。
◎三平方の定理とは?簡単にわかりやすく定義をご紹介
三平方の定理とはどのようなものか簡単にみていきましょう。三平方の定理で定義されているのは、直角三角形の三辺の長さに成り立つ関係式です。直角三角形の一番長い辺の長さを2乗したものが他の辺の長さを2乗したものの合計と一致します。たとえば、最も長い辺の長さをa、その他の辺の長さをb.cとすると、必ずa²=b²+c²になるということです。
◎三平方の定理とピタゴラスの定理の違いとは?
ピタゴラスの定理について中学などで言葉を聞いたことがあるかもしれません。三平方の定理とピタゴラスの定理にどのような違いがあるのか気になるところですが、実は同じものです。三平方の定理を発見したピタゴラスは、紀元前に古代ギリシャで活動した数学者であり、発見者の名前をとってそのような名前でも呼ばれています。また、平方根の定理も、三平方の定理の別名です。
◎三平方の定理で整数比・整数解として有名なものは?
三平方の定理でよく出てくる整数の一覧が気になるかもしれません。三平方の定理は各辺が整数の比にならなくても正の実数であれば成り立ちます。ただ、三平方の定理で整数解になるものは問題として利用されやすいので、計算のスピードを上げる点でも覚えておいて損はないでしょう。三平方の定理の整数比としてよく出てくるのは、3.4.5・5.12.13・8.15.17・7.24.25などです。それぞれ●倍したものとして出題されることも多いため、直角三角形でかつ比率のうちどれかが一致する場合は、「三平方の定理の整数の比を使うのかな?」と考えてみても良いかもしれません。
◎三平方の定理で角度から計算できてしまう?
三平方の定理では角度から長さを求めることも場合によってはできます。三平方の定理を使った角度からの計算もあわせておさえておきましょう。最も有名なのは角度が90度・45度・45度の直角二等辺三角形です。辺の長さが√2:1:1なので、三平方の定理を使えば一辺しかわからないときでも求められます。
また、角度が90度・60度・30度の特殊な直角三角形の辺の長さの比は√3:√2:1です。これを応用できるのが、正三角形の底辺の長さでしょう。対頂角から底辺に線を引くとこれが垂線になる(詳細)ため、90°・60°・30°の直角三角形が内部にできるからです。三平方の定理を使えば、角度の求め方として出てくる高校数学の方法を使わずに解けることもあります。
◎三平方の定理は身の回りでどんなことに使われている?
三平方の定理は身の回りの様々な場面で利用されています。小学生の頃に使った三角定規2種類はピタゴラスの定理をもとに三辺の長さの比率が決められているものです(先ほど紹介した√2:1:1と√3:√2:1)。また、パソコンやテレビは対角線でインチを表示しているため、三平方の定理を応用すれば縦と横の長さが大体わかります。また、高さがある木やビルについても、角度を基にそこまでの距離をはかることで計算でき、直接計測する必要はありません。このように、単に数学の世界だけでなく、三平方の定理は身の回りの測量でも大いに役立っているのです。
◎三平方の定理/ピタゴラスの定理を図解すると?
三平方の定理を図解してみましょう。エクセルで図(オートシェイプ)を挿入しましたので、こちらを使って解説していきましょう(Excelの図形は見やすいように6.8.10セルで表記)。
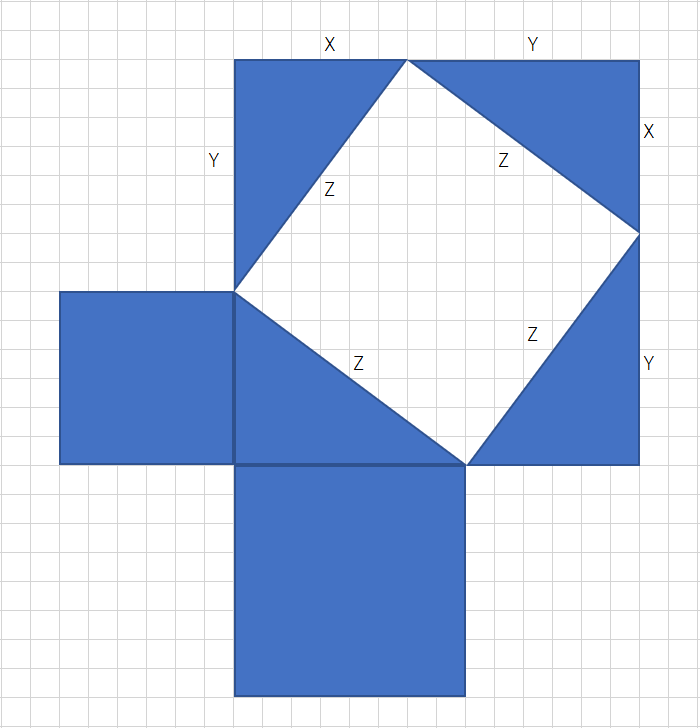
直角三角形の角度を90度ずつ動かし、左の図のように長辺の頂点二つを異なるように並べます。すると、1辺が(X+Y)の正方形が外側にでき、面積は(X+Y)²:①
です。一方で、内側にある正方形は、直角三角形で一番長い辺に該当し、その面積はZ×Z=Z²:②と表されます。
大きな正方形から小さな正方形を除いたのが直角三角形4つ分ですから、式は
(大きな正方形の面積)-(小さな正方形の面積)=X×Y÷2×4=2XY:③
です。文字式の展開公式を利用すると、
①は(X+Y)²=(X+Y)(X+Y)=X²+XY+XY+Y² (←大きな正方形の面積に該当)
なので、②③合わせて(X+Y)²-Z²=2XYより、X²+XY+XY+Y²-Z²=2XYで、
三平方の定理であるX²+Y²=Z²が導き出せました。ちなみに、右の図のように直角三角形の頂点を結んで正方形を半分にし、台形の面積を求める方法でも三平方の定理が出て
きますので、気になる場合は試してみましょう。
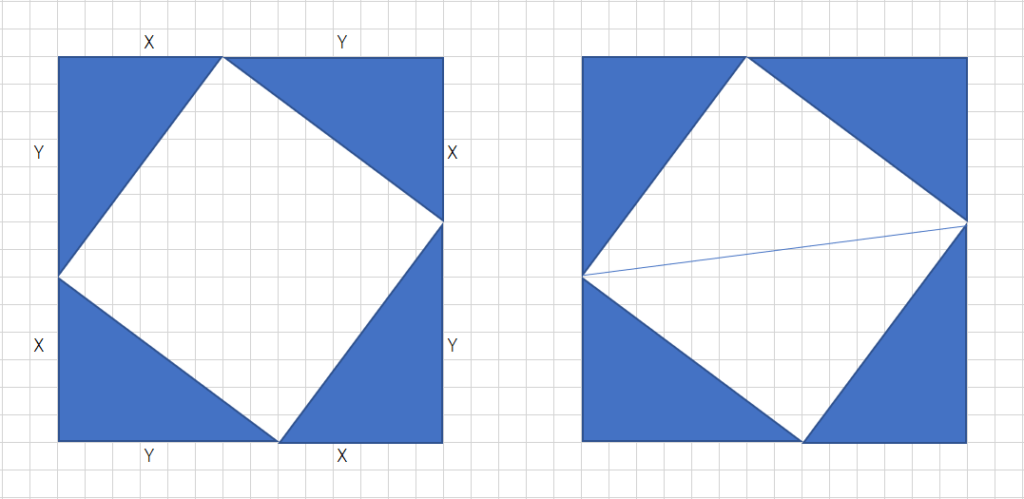
ピタゴラスの定理の図解としては、90度ずつ回転させて四つ並べた直角三角形を使うのもおすすめです。直角ではないのように直角ではない頂点同士をつなげるようにして並べると、短い2辺の長さの合計が計算できるので、そこから4つの直角三角形を引くと正方形の面積です。小学校でも学ぶ面積の公式を使い、底辺6.8の直角三角形なら大きな正方形=(6+8)×(6+8)=196、三角形の面積=6×8÷2=24で直角三角形の長辺を1辺とする正方形=196-24×4=100で確かに10の2乗になっていますよね。

◎ピタゴラスの定理についての証明、中学生でできるものは?
ピタゴラスの定理の証明は中学生であればおさえておきたいかもしれません。様々な方法がある中でおすすめとしては、直角三角形の相似比と面積比を使う方法が挙げられます。三角形の相似とは、3つの角が等しい場合に必ず形が同じであるため、各辺が同じ倍率だけ拡大または縮小すると一致する性質です。また、三角形の面積比は、相似比の2乗であることを利用します。
以下の図を使って導き出してみましょう。直角三角形のうち、角度が90°の頂点Aから対辺へ垂線(角度が90度になるような直線)をおろし、その点をDとします。こうすることで、内側にさらに2つの直角三角形ができますよね(90°の角は桃色の■で表しています)。また、角度を見てみると、茶色の直角三角形のうち左側の角度(黄色の○)は紫色の直角三角形の○と同じものであり、右側の角(水色の☆)は黄緑色の直角三角形の☆と同じものです。
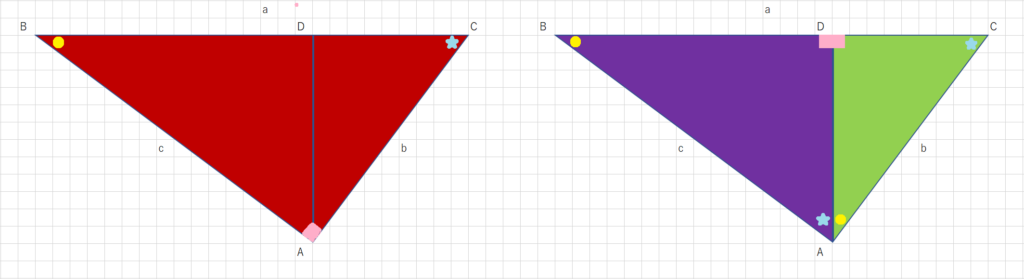
したがって、茶色と紫色・茶色と黄緑色の三角形は二つの角度が等しく、引き算をすると3つ目の角度も同じなので、いずれの直角三角形も相似であるとわかります。斜辺(直角の頂点の対辺)の長さをそれぞれa.b.cとすれば、相似比がa:b:cで表せるので、面積比は2乗のa²:b²:c²です。大きな直角三角形は小さな直角三角形を合わせたものですから、三平方の定理であるa²=b²+c²が成立すると証明できました。
◎ピタゴラスの定理の証明は小学生の算数でもできる?
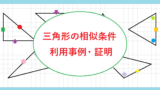
ピタゴラスの定理の証明はいろいろあり小学生の算数の内容でも可能です。直角三角形4つ並べて外側と内側に正方形を作った図を使ってみましょう。このうちオレンジの直角三角形を赤の直角三角形と斜辺がくっ付くように動かします。同じ大きさ形の直角三角形ですから、ぴったりと一致しますよね。同じように紫の直角三角形を動かして黄緑の直角三角形と合わせます。余った部分に2つの正方形ができているのがわかりますか?同じ大きさ形の直角三角形のうち、短いもの同士の辺、長いもの同士の辺の正方形です(下側はオレンジの三角形の短い方の辺と紫の短い方の辺による正方形)。
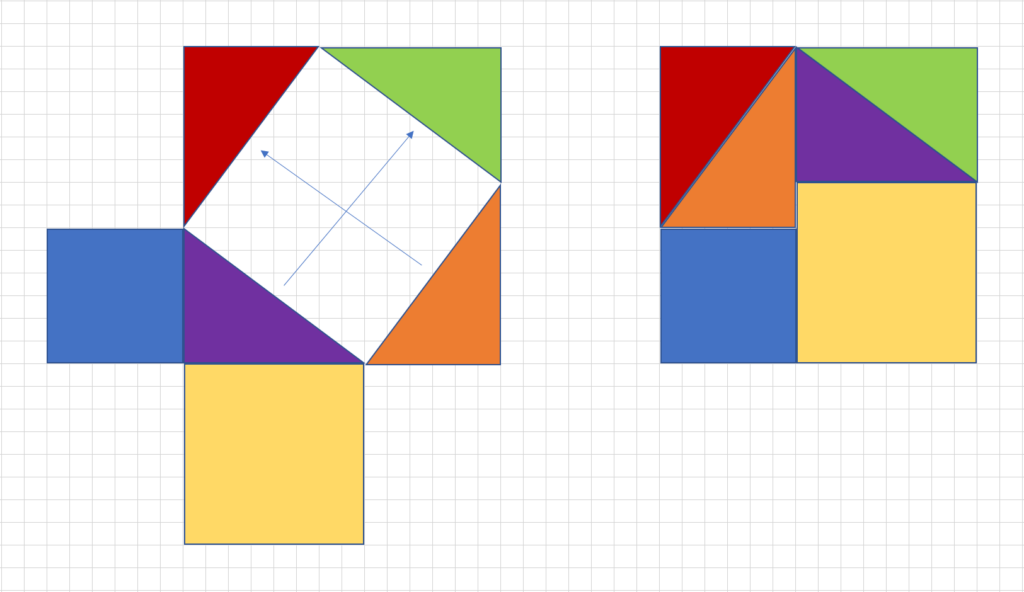
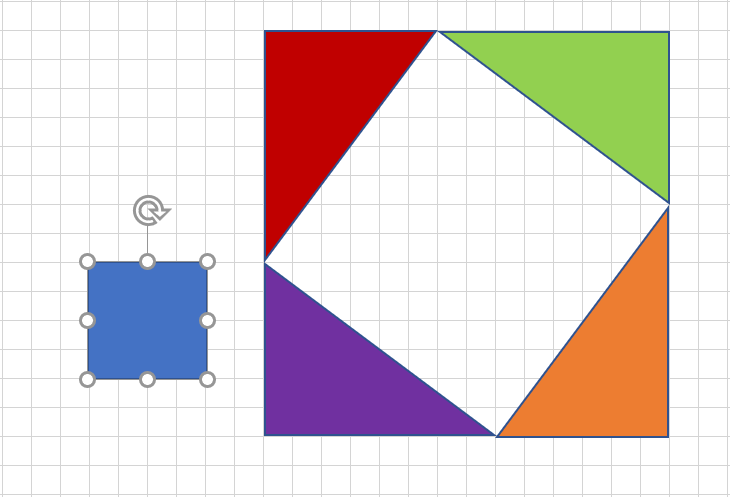
この2つの正方形は、大きな正方形から赤・オレンジ・黄緑・紫の4つの直角三角形を引いたものですから、左側の図にある小さな正方形と一致します。この小さな正方形は直角三角形の一番長い辺を一辺としますから、直角三角形の一番長い辺の2乗が他の二辺をそれぞれ長さとする正方形の合計に一致することがわかり、三平方の定理が証明できました。
◎まとめ
今回は、三平方の定理とはどのようなものかについてわかりやすくご紹介しました。三平方の定理は整数の比は一覧で押さえておくと数学以外の場面でも便利かもしれません。特殊な直角三角形で利用できたり角度を求めることをしたりするなど使い道も多いので図を使って考えることも押さえながら活用しましょう。最後までお読みいただきありがとうございました。
関連記事:三平方の定理の性質を利用した問題はどんなものがある?