合同三角形とはどのようなものかが気になるかもしれません。中学数学では合同条件が出てきますので、一覧や証明の書き方も把握しておきたいですよね。三角形の合同条件を証明するときのコツは、合同な図形で対応する辺の順番や角の順番に注意を払うことなどいくつかあるのが特徴です。今回は、三角形の合同条件の練習問題(三つの角が等しい三角形は正三角形である証明など)を、直角三角形の合同と証明もあわせてご紹介します。
◎合同三角形とは・三角形の合同条件とは?覚え方
合同三角形とは、回転あるいは裏返すことなどで位置や向きを変えることで完全に一致する二つの三角形です。三角形の合同条件とは、そのような関係になるために満たすべき条件のことを指します。合同条件の一覧は、次の通りです。
・三辺相等 ・二辺夾角相等(✖にへんそうかく) ・一辺両端角相等
三角形の合同条件は高校の数学でも応用できるので忘れないようにしたいかもしれません。三角形の合同条件の覚え方としておすすめなのが、まず三角三辺の長さのうち3つを使っている点を押さえます。その上で、2組にするのが角度か辺の長さかによって、その間の辺or角も必要だと考えるのが良いでしょう。

●[中学数学]三角形の合同条件として3つの角は?中3数学の相似条件
また、三角形の合同条件として3つの角が等しいは含まれません。以前ご紹介した三平方の定理の図形を例にしてみると、直角二等辺三角形は角度が90度・45度・45度です。しかし、辺の長さの比が√2:1:1なので、短い辺の長さによって様々な大きさの三角形が考えられ、一通りに決まりません。3つの角が等しいというのは中3数学などでの相似条件であり、3辺の長さが一定の比率の関係を指します。

◎合同な図形で注意したい対応する辺の順番
合同条件の証明や問題を解く際には、対応する辺や角の順番を一致させることが重要です。たとえば、三角形ABCと三角形DEFが等しいときには、辺ならAB=DE・BC=EF・CA=FD、角度なら∠BAC=∠EDF・∠CBA=∠FEDなどと表記します。特に三角形の証明で条件∠CBA=∠FEDのところを∠ABC=∠FED・AB=DEではなくAB=EDと書くと、合同な図形で対応する辺の順番や角の順番がわかっていないと判断される(減点される)可能性が高いです。「∠BCAだから対応する方も2番目3番目1番目の順に書く」などと毎回決めて慎重に記入するようにしましょう。
◎三角形の合同の証明問題、三角形の合同条件の証明のコツは?
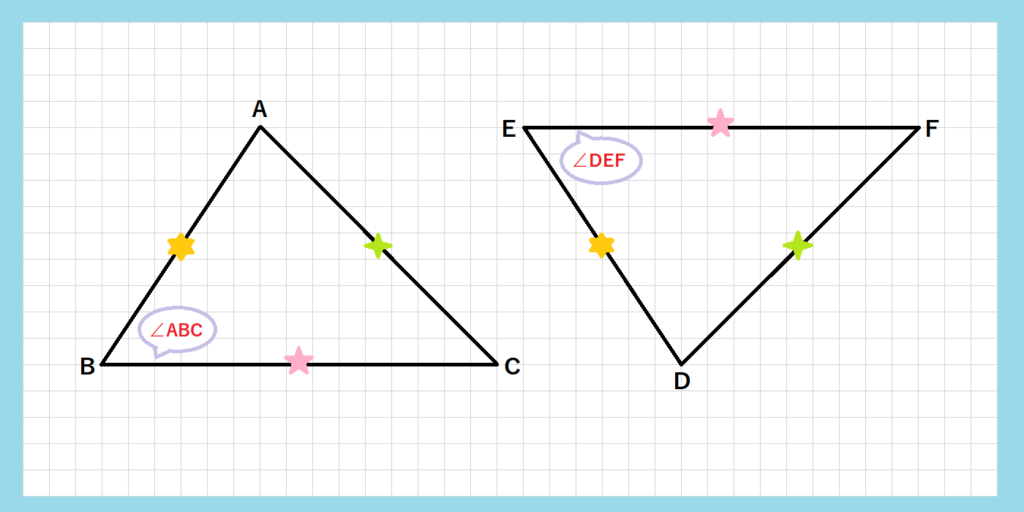
中学数学では、三角形の合同の証明問題やそれを使って別のことを示す場合もあるかもしれません。三角形の合同条件での証明のコツとしては、条件を正確に選び、順序立てて証明を進めるが挙げられます。例としては、図に補助線を引いて対応する辺や角が何なのかをはっきりさせることが挙げられます。対応するものに数字あるいは異なる種類の記号(●・▲・★など)を書き込むことで、ミスも避けられる可能性が高まるでしょう。
◎三角形の合同の利用問題
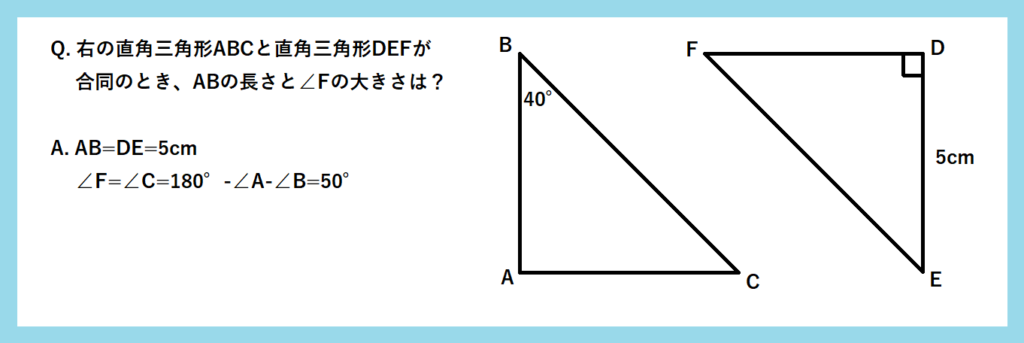
三角形の合同の利用問題はどのようなものがあるのかは、応用問題まで対策する上で気になるかもしれません。合同条件の証明を自然と使えるようになるには、実際にどのような例があるかを把握しておくことも重要です。三角形の合同条件の練習問題として3つご紹介しましょう。三角形で対応する辺や角度を求めるものからです。
●[中学数学]合同での証明問題を利用した、台形の性質
三角形の合同の利用問題では、四角形をはじめとする多角形の中で性質を使う場合があります。ここでは、台形の面積の公式がなぜ(上底+下底)×高さ÷2なのかをみていきましょう。

●三つの角が等しい三角形は正三角形であることの証明
三つの角が等しい三角形は正三角形であることの証明も、利用問題の一例としてあわせてみておきましょう。三角形PQRにおいて、三角が等しいことから∠P=∠Q=∠Rが与えられています。ここで、Rの内角二等分線とPQの交点をSとしましょう。∠PRS=∠QRS=0.5×∠Rであることから△PRSと△QRSの残りの角度も等しい(∠RSP=∠RSQ=90°)も成り立ちます。また、RSは共通していることから△PRSと△QRSが二角夾辺相等の合同三角形となり、対応するPRとQRも同じ長さです。

同様に、∠Q=∠Rと、∠Pの内角二等分線とQRの交点をTとしたときに、△QPTと△RPTが二角夾辺相等の合同三角形となり、対応するPQ=PRが成り立ちます。したがって、3つの角が等しい三角形は正三角形であることが示せました。
◎直角三角形の合同と証明
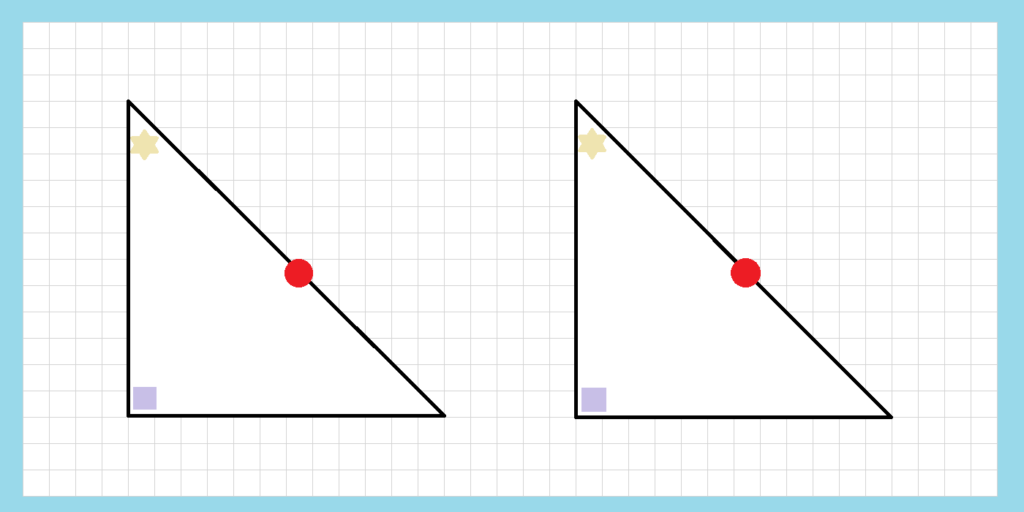
直角三角形の合同は証明するにおいても少し特殊です。斜辺と他の1辺がそれぞれ等しい」「斜辺と他の1つの角度がそれぞれ等しい」の2つがあります。「斜辺と他の1つの角度がそれぞれ等しい」ことは、三角形の内角の和が180°であることより残りの角度も等しく、「一辺の長さと両側にある角がそれぞれ等しい」合同条件に該当するためです。
中2数学の証明でも出てくる直角三角形の合同の示し方もみていきましょう。三角形ABCと三角形DEFにおいて、∠A=∠D=90°・斜辺BC=EF・他の1辺;AB=DEとあてはめました。等しい他の1辺同士を直角部分が同じ方に来るように重ね合わせると、AとD・BとEがそれぞれ一致し、∠A+∠D=90°×2=180°でC.A.D.Fが一直線上にあります。斜辺同士が等しいこと(BC=EF)から三角形BCF(ECF)は二等辺三角形の成立条件を満たしており、底角が等しく∠C=∠Fです。したがって、残りの角度も等しく∠B=∠Eであることから、「一辺の長さと両側にある角がそれぞれ等しい」とわかりました。

◎まとめ
今回は、三角形の合同条件について証明での注意点やよくある例題をご紹介しました。三角形の合同条件がほかにもないのかが気になったかもしれません。他の条件が当てはまらないことを示すには、全ての場合を挙げて反例(仮定している条件が成り立たない事例)を出していく必要があります。詳しくはこちらの記事で触れていますので、参考にしていただけますと幸いです。最後までお読みいただきありがとうございました。



