方べきの定理が中学や高校入試問題でどう出てくるのかが気になるかもしれません。
ほうべきの定理の証明で中学生の段階でもわかるものがあれば、方べきの定理の覚え方にこだわる必要もないですし、理解が深まりますよね。今回は、ほうべきの定理の例題や応用問題と半径や比を絡めたもの、方べきの定理の逆とは何かなどをわかりやすくご紹介します。
◎ほうべきの定理は漢字で意味がわかる、接線と比の条件
ほうべきの定理は漢字では[方冪の定理]です。方べきの定理は、英語では[Power of a point theorem]と表記します。冪およびpowerは数学用語では累乗の意味です。図形の性質のひとつである方べきの定理における方べきとは、円周上にない点から円の中を通る直線を引いた際の円と交点の距離の積を指します。方べきの定理とは簡単にいうとこのように定義された方べきが必ず一定であることです。たとえば、以下の図形であればXの位置に関係なく、XP×XQ=XR×XSが成立します。
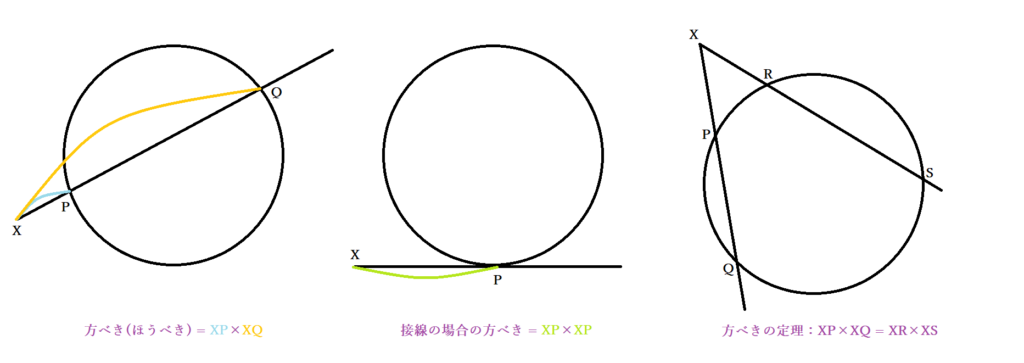
ほうべきの定理は比の話だというのは、この式を入れ替えたXP:XR=XS:XQも成り立つことからわかるでしょう。方べきの定理の覚え方として接線のときもあわせて押さえるのをおすすめします。例として以下のように円の接線のとき、XP×XQ=XP²からXP²=XR×XSです。方べきの定理はいつ習うのかというと、文部科学省の指導要領では高校数学Aの平面図形に含まれています。数aで方べきの定理は多角形が円に内接する条件など図形の特徴を学ぶ問題や証明にあたり出てくることが多いです。ただし、円周角の定理など円の性質として方べきの定理が取り上げられ、進度が速いと中学2年生あたりで出てくることもあるでしょう。
◎図形の性質:方べきの定理と円の中心と半径の関係
ほうべきの定理が半径とどのような関係なのかが気になるかもしれません。結論から言えば、方べきの定理から円の中心などが直接求められるわけではないですが、円の中や外での線分の長さの関係を示すことで特定の点や円の性質の情報を求めるのに役に立ちます。方べきの定理で円の外部にある点から接線を引いたときの長さを求め、半径などはピタゴラスの定理などを使って求めるのが例の一つです。
◎三平方の定理の証明が方べきの定理を使ってできる?
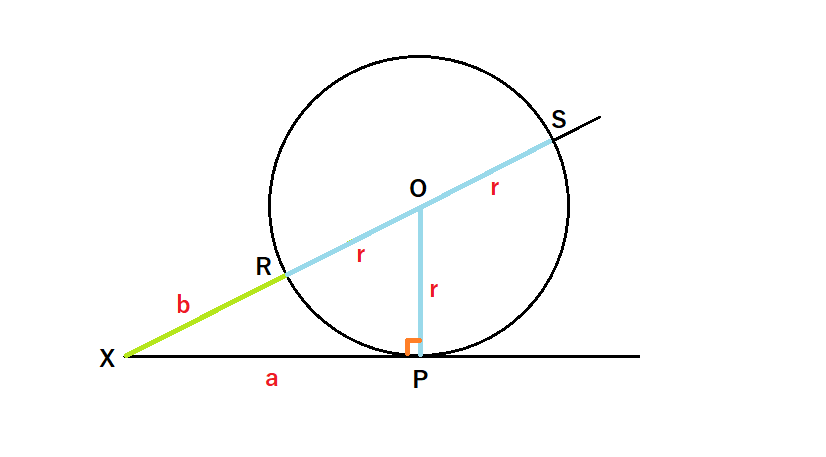
以前の記事で、三平方の定理の性質について触れていました。三平方の定理の証明は方べきの定理を使うことでもできます。使うのは、以下のように2本の直線のうちの片方が円の接線、もう片方が円の中心を通っているものです。ここで円の半径=r・XP=a・XR=bとおくと、ほうべきの定理よりXP²=XR×XSなので、a²=b×(b+r+r)と表せます。式を整理して、a²=b²+2br=(b+r)²-r²です。(b+r)=OX・r=OPなので、直角三角形OPXでOP²+XP²=OX²が成り立ち、三平方の定理が示せました。
◎ほうべきの定理の例題・中学生でもよくみる問題
ほうべきの定理にはどのような例題があるのかが気になるかもしれません。数学の方べきの定理は高校入試問題にも出てくる可能性があり、応用や難問にも対応できるようにはしていきたいですよね。ほうべきの定理での中学生でもみる応用問題も含めた例をご紹介しましょう。

応用としては、方べきの定理以外の定理・定義も絡めて解くものがあります。また、逆から角度を求めたり2つの円の4点が同一円周上にあることを示すなども頻出です。証明については、次の項目でみていきましょう。
◎円の性質:方べきの定理の証明(中学)
今回はわかりやすいように、直線を引く基準の点をX・異なる2つの直線と円の交点のうち片方をAとB・もう片方をCとDとしました。なお、XがABおよびCDの間にあるとき、AとDは直線BCで区切ったときに同じ側です。ここでは円周角の定理として、同一弦からの円周角がいずれも等しいことと、内接四角形の対角の和の関係性を利用しています。
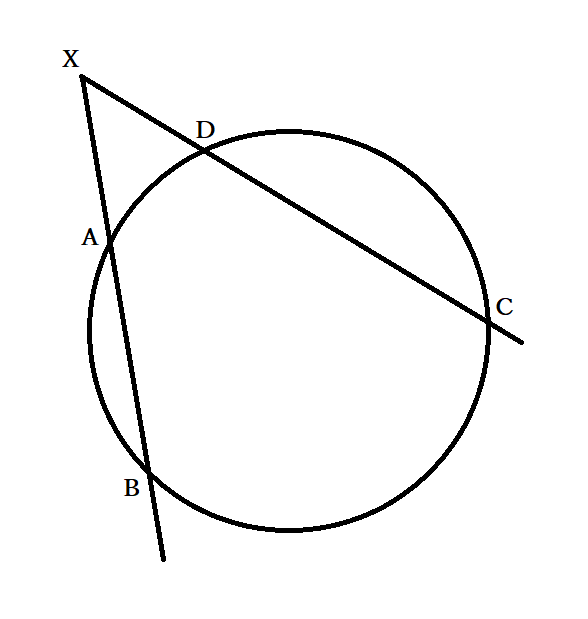
●基準の点が円の内側にあるとき
Xは線分ABおよび線分CDの間にあります。円周角の定理より∠XAC=∠XDB・ ∠XCA=∠XBDが成り立つので、 三角形XACと三角形XDBは相似です。相似な三角形は辺の長さの比が等しいので、AX:DX=CX:BXの関係が成立します。よって、AX×BX=CX×DXとなりました。
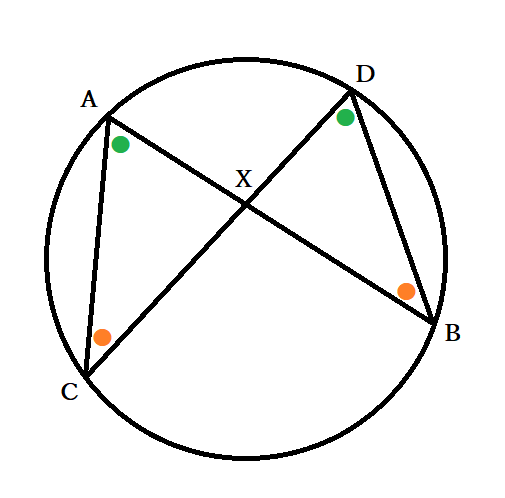
●基準の点が円の外側にあり、点からの2直線が円と2つずつ交点を持っている場合
Xに近い側の点同士(AとD)・遠い側の点同士(BとC)を結びましょう。円周角の定理より円に内接する四角形の対角の合計は180度なので、∠DBA+∠DCA=180°・∠BAC+∠BDC=180°が成り立ちます。また、直線は180度より∠XAC+∠BAC=180°・∠XCA+∠DCA=180°です。したがって三角形XACと三角形XDBにおいて∠XBD=∠DBA=180°-∠DCA=∠XCA・∠XDB=∠BDC=180°-∠BAC=∠XACより相似なので辺の比からXA:XD=XC:XBで、AX×BX=CX×DXとなりました。
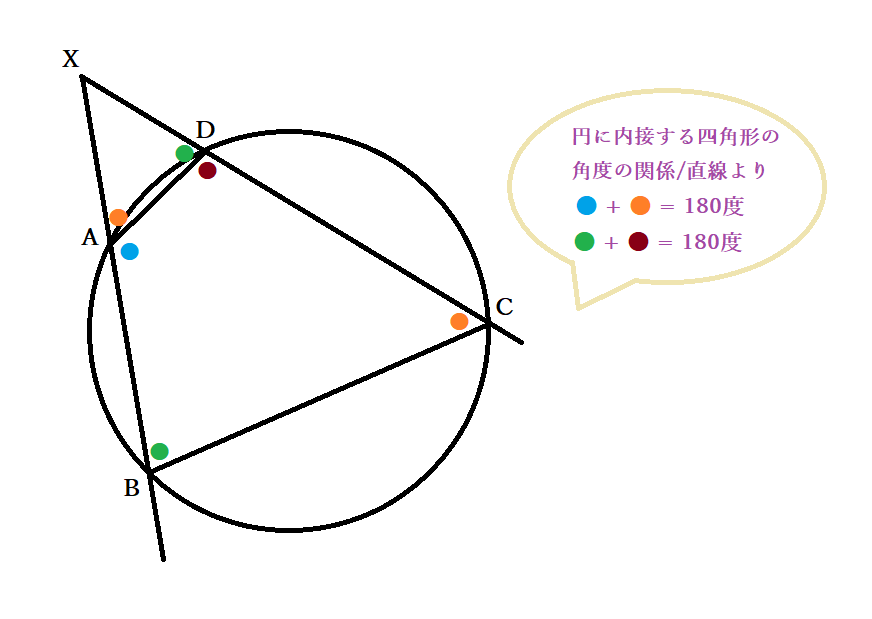
●基準の点が円の外側にあり、点からの2直線の一方が円の接線である場合
C=Dだと考えます。三角形XACと三角形XCBにおいて接弦定理より∠XCA=∠XBCが成り立ち、∠Xは共通角なので∠AXC=∠CXBです。したがって三角形XACと三角形XCBは相似なので、XA:XC=XC:XBで、AX×BX=CX×DXとなりました。
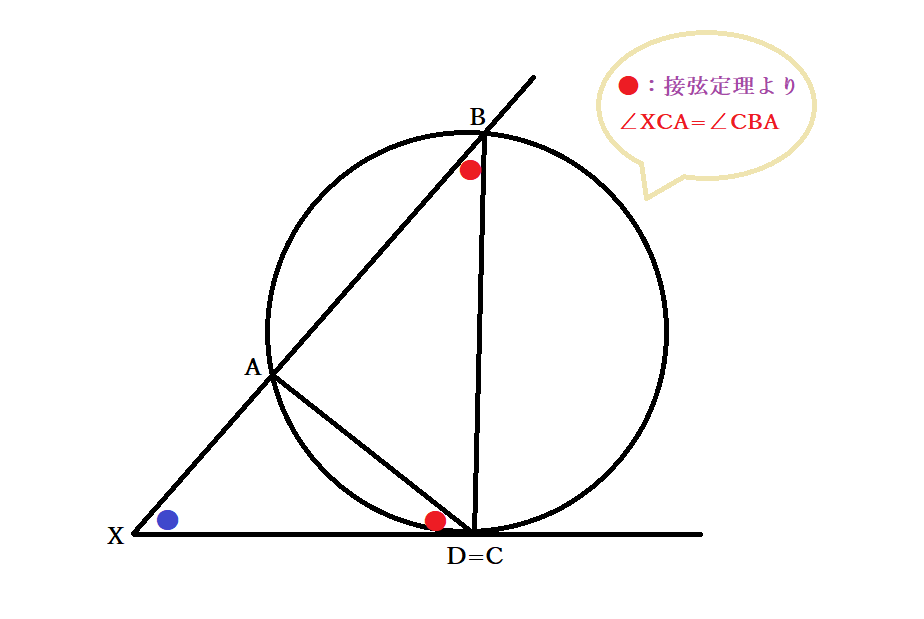
●基準の点が円の外側にあり、点からの2直線がともに接線である場合
円の外側の点から円に2つの接線を引いたときもまた、方べきの定理が成り立ちます。円と直線の交点は1つだけですから、A=B・C=Dとして考えると、合同条件よりXA=XCとなり、AX×BX=CX×DXを満たすのです。
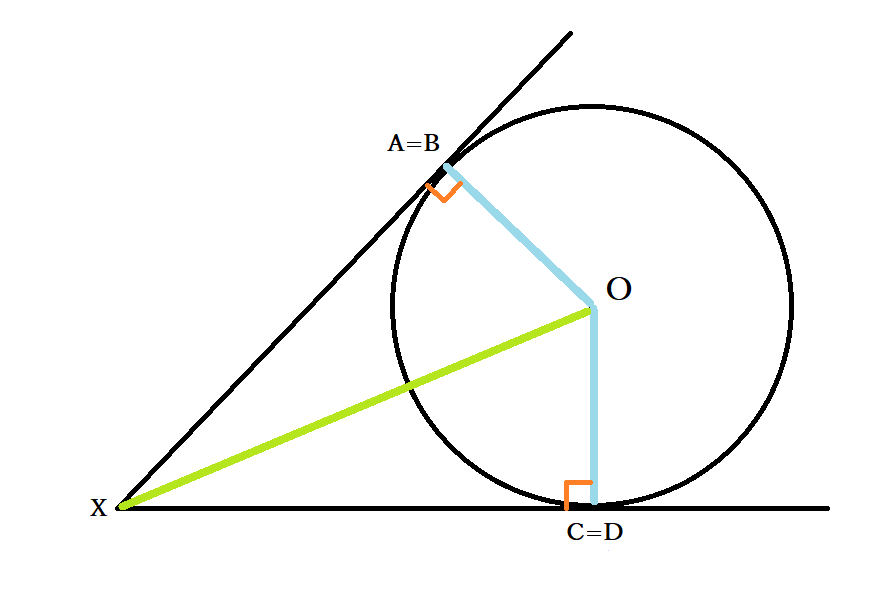
◎方べきの定理の逆とは?角度と比をつかって接線の存在を示す
方べきの定理の逆とはどのようなものかが気になるかもしれません。方べきの定理では比を求めていましたが、長さと角度によって接線の存在を導く流れになります。具体的には、『直線ABと直線CDがXで交わるとき、AX×BX=CX×DXの関係性が成り立つ4点A.B.C.Dが同一円周上に存在する』ことを示しましょう。
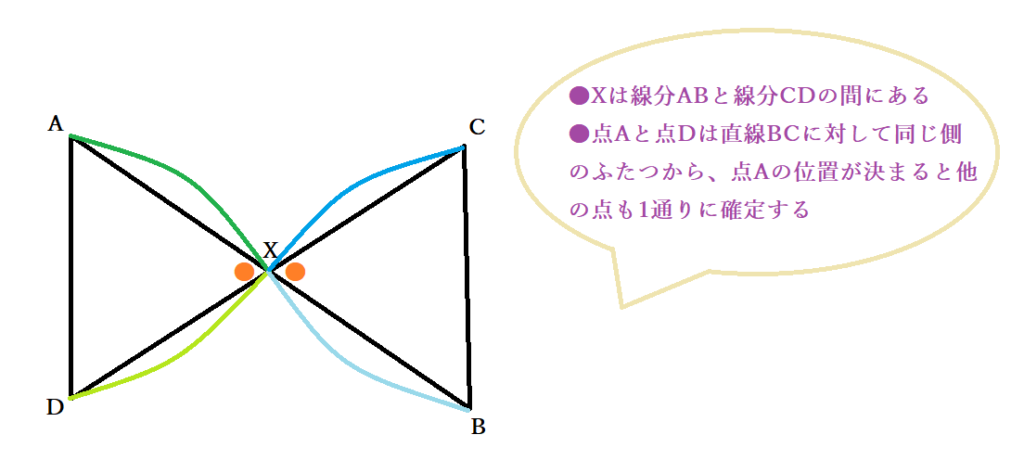
●Xが線分ABおよび線分CDの間にある場合
AX×BX=CX×DXが成立するとき、AX:CX=DX:BXです。また対頂角が等しいので∠AXC=∠DXBで、この二つから三角形XACと三角形XDBは相似だとわかります。よって、∠XAC=∠XDBが成立し、円周角の定理の逆より4点A.B.C.Dが同一円周上に存在すると示せました。対応する角が弦の直線に対して同じ側にあることが条件ですが、AとDは直線BCで区切ったときに同じ側にあるものとしているので満たしています。
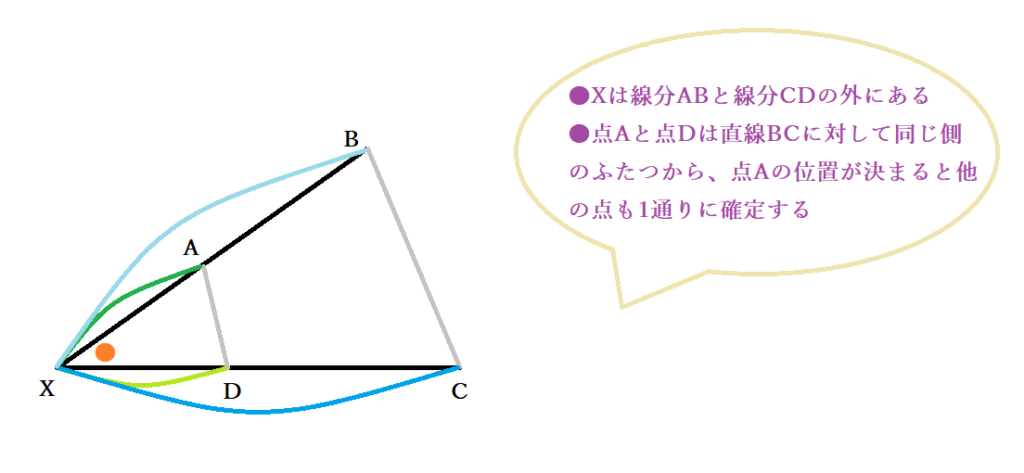
●Xが線分ABおよび線分CDの外にあり、4点がいずれも異なる点である場合
同様にAX:CX=DX:BXと、共通角∠AXC=∠DXBであり、三角形XACと三角形XDBは相似だとわかります。よって、∠XAC=∠XDBが成立し、∠BAC=180°-∠XAC= 180°- ∠XDBより ∠BAC+∠CDB=180°です。したがって、四角形ACDBの対角が180°であることから、4点A.B.C.Dは同一円周上にあることがわかりました。
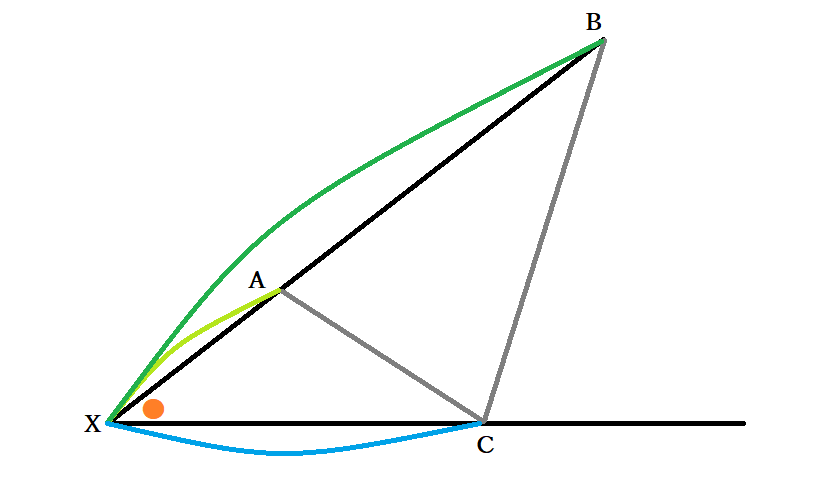
●Xが線分ABおよび線分CDの外にあり、C=Dである(片方だけ2点が一致している)場合
C=Dの場合のみを取り上げます。AX:CX=CX:BXと共通角を持つことから∠AXC=∠CXBであり、三角形XACと三角形XCBは相似なので∠XCA=∠XBCです。よって、接弦定理の逆よりA.B.Cは同一円周上にありかつXCが接線であることが分かりました。
●Xが線分ABおよび線分CDの外にあり、A=B・C=Dである場合
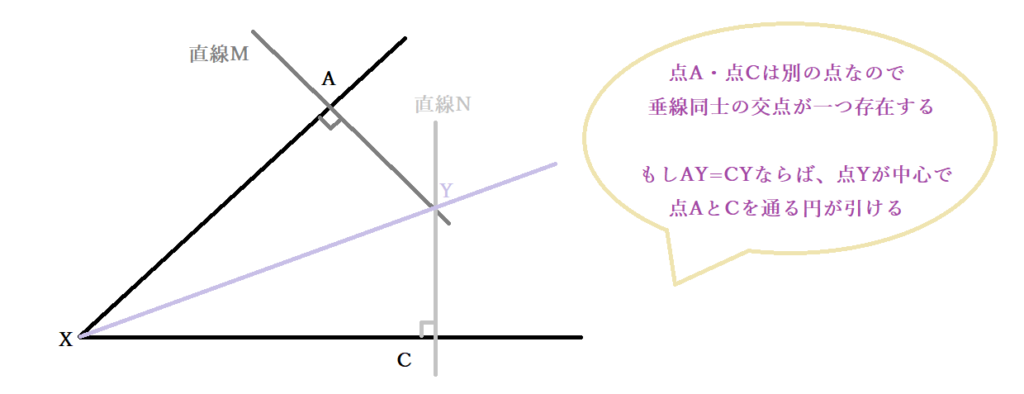
2点A.Cの両方を通る円が存在することは明らかでしょう。求めるべきものは、先ほどの4番目の逆条件ですから、XAとXCが接線となる円が存在するかです。試しに、Aを通りXAと垂直に交わる直線MとCを通りXCと垂直に交わる直線Nを考えます。XとAとCはいずれも異なる点でかつXを交点に持つのでXAとXCは完全一致でも平行でも垂直でもなく、共に垂線である直線Mと直線Nの交点も1つです。その点をYとすると、三角形XAYと三角形XCYは、XY共通・条件XA×XA=XC×XCよりXA=XC・∠XCY=∠XAY(Yは垂線M.Nの交点だから)が成り立つことより直角三角形の斜辺と他の一辺がそれぞれ等しいので合同だとわかりました。したがって、YA=YCでYからも2点A.Cを通る円が引け、なおかつ∠XCY=∠XAY=90°なので XAとXCが接線となる円は存在します。
◎まとめ
今回は、方べきの定理について証明(中学)や応用問題もあわせてわかりやすくご紹介しました。三平方の定理の証明にも方べきの定理は使われることもあり、円の中心や半径などを比から求めるのに役立つこともあります。証明そのものは円周角の定理・接弦定理・2接線と円の関係など平面図形の要素がいくつも絡まる点で複雑です。もしよくわからない場合には、それぞれの定理に戻ってじっくりと理解していくと良いでしょう。最後までお読みいただきありがとうございました。