接弦定理を中学や高校で習う際にどう証明するかが気になったかもしれません。求め方やポイントを知って知っておくと暗記に頼る必要もないですし、理解が深まりますよね。今回は、接弦定理とは何かに関して、わかりやすく考えられる覚え方や例題、証明方法などをご紹介します。
◎接弦定理(せつげんていり)とは?円の接線と弦のつくる角の定理
接弦定理(せつげんていり)は「円の接線と弦の作る角の定理」を短くしたものです。「円の接線と弦のつくる角の性質」などとと呼ばれることもあります。接弦定理の正式名称ははっきりしませんが、文部科学省の記載に則るなら『円の接線と接点を通る弦とのなす角の性質』でしょう。
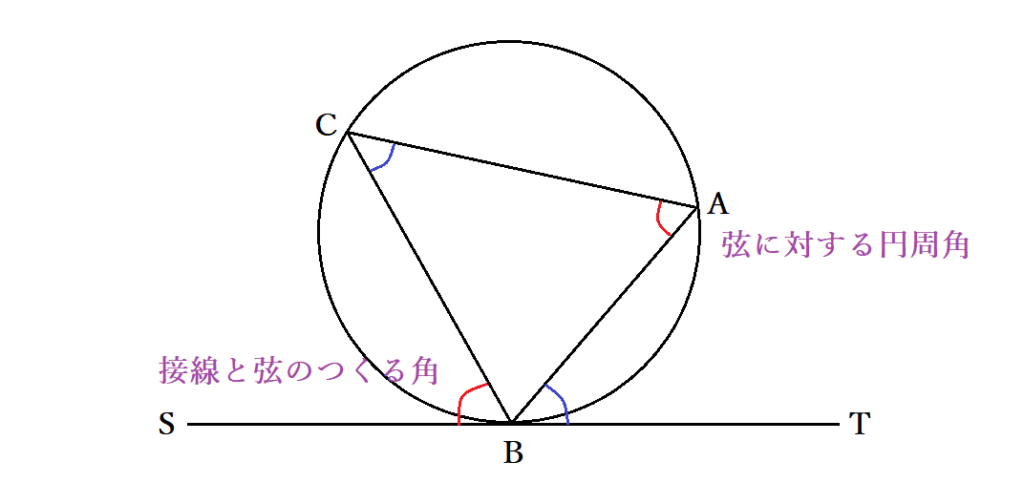
接弦定理とは、接線と弦に関する定理の意味です。円の接線と弦のつくる角と弦に対する円周角が等しいことを指します。たとえば、円に内接する三角形ABCとBを接点とする接線上の点をS.Tとしましょう。このとき、接線と弦の作る角とは∠SBCで、弦に対する円周角は∠BACです。接弦定理では∠SBC=∠BACが成り立ち、同様に∠TBA=∠BCAも成立します。
◎接弦定理はいつ習う?中学、それとも高校?
接弦定理(接線と弦の作る角の定理)をいつ習うのかが気になるかもしれません。接弦定理という名称は文部科学省の指導要領にはなく、略称です。平成30年(2018年)告示の高等学校学習指導要領では、「数学A;円の性質」の一例として「方べきの定理」などと並び「円の接線と接点を通る弦とのなす角の性質」との文言があります。後ほどご紹介しますが、円周角の定理と接線の性質から接弦定理を導くため、円と三角形の性質の応用として取り上げられることもあり、進度が速いと中学2年生で出てくることもあるようです。
◎接弦定理の覚え方:接線と弦のなす角を決めるのがポイント
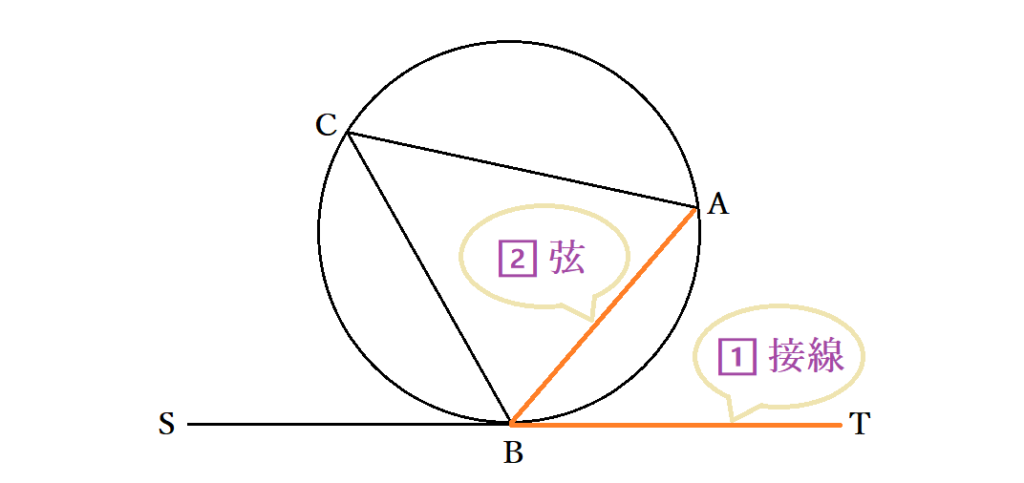
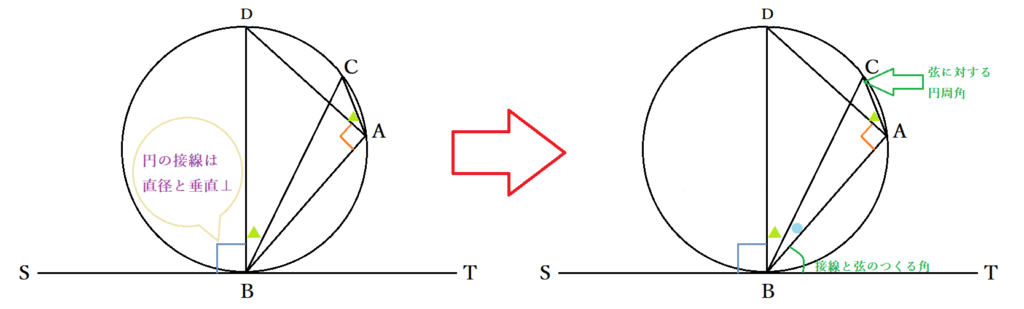
接弦定理の覚え方も押さえておきたいかもしれません。円の接線と弦の作る角がわかりやすく導ける方法を把握していると、証明問題の際に怪しくなっても落ち着いて考えられますよね。接弦定理の覚え方は、接線と弦のなす角を決めるのがポイントです。まず、円の接線と弦のつくる角を探します。接線がBTのとき、接線と弦の作る角は∠TBAなので弦はABです。
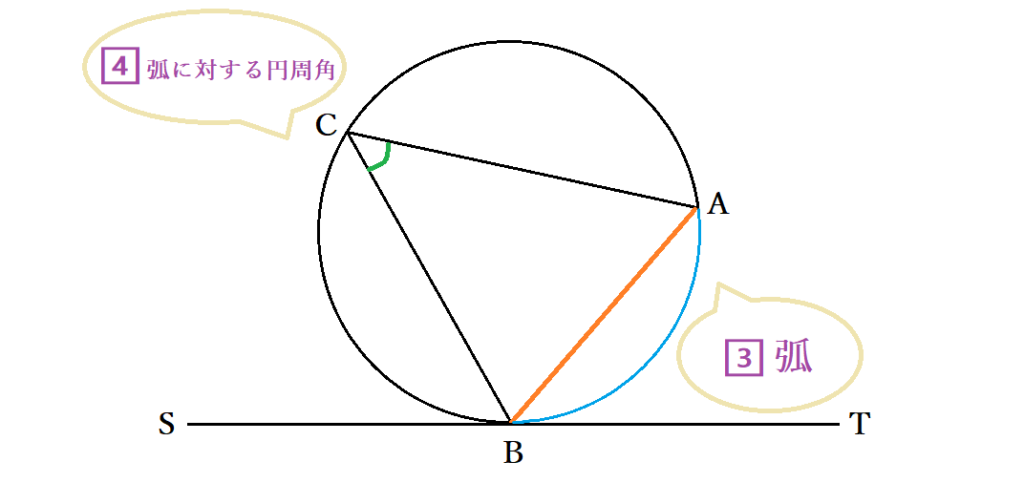
弦が決まれば、円周上の弦に対する弧を見つけ、弧にある円周角を探します。ここでは、弦ABに対する弧は色を付けた部分で弧に対応する円周角は∠BCAです。
◎接線と弦の作る角の定理の証明:円周角の定理と接線の性質を利用
接弦定理がなぜ成り立つのかは、円周角が鋭角(90度未満)・直角(90度)・鈍角(90度より大きい)の3通りで分けて証明します。円周角がどのようなものなのか・円周角の定理の証明方法に関しては、こちらの記事も参考にしていただけますと幸いです。
●接弦定理の証明:鋭角の場合
円の中心Oおよび接点Bを通る直線を引き、B以外の円との交点をDとおきます。ここで、DBは円の中心Oを通っているので円の直径ですから、円周角と中心角の関係より∠BAD=90度です。∠BCA=●とおくと円周角の定理より弦が共通している円周角の大きさは等しいので、∠BCA=∠BDA=●が成り立ちます。よって、三角形ABDにおいて∠DBA=180°- ∠BDA- ∠BAD=180°-●-90°=90°-●です。
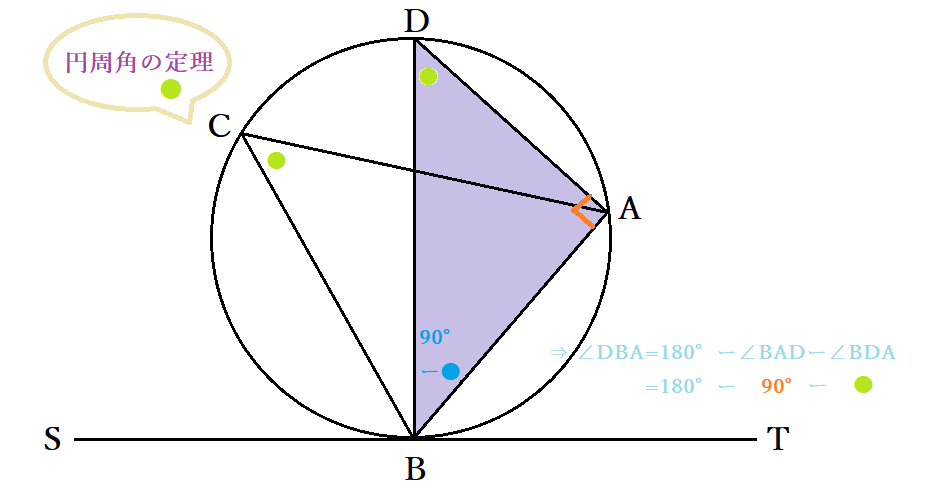
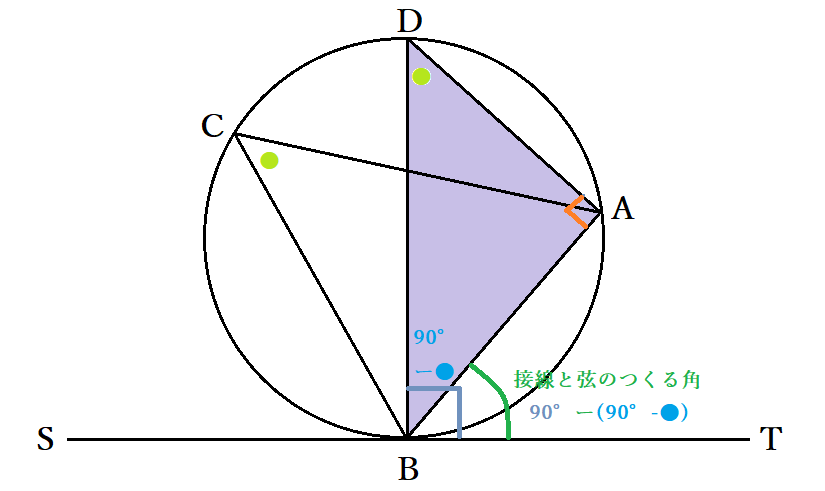
他方、BDは円の直径であり、接線と90度に交わることから、∠TBO=90度も成り立ちます。したがって、∠TBA= ∠TBO-∠ABO=90°-( 90°-●)=●で、 ∠BCA=∠BDA= ∠TBAだとわかりました。三角形の内角の和が180度・直線をなす角度が180°であることから他の部分を除いて、∠BAC=180°-(∠ABC+∠BCA)= 180°-(∠ABC+∠TBA)=∠SBCも成り立ちます。
●接弦定理の証明:直角の場合
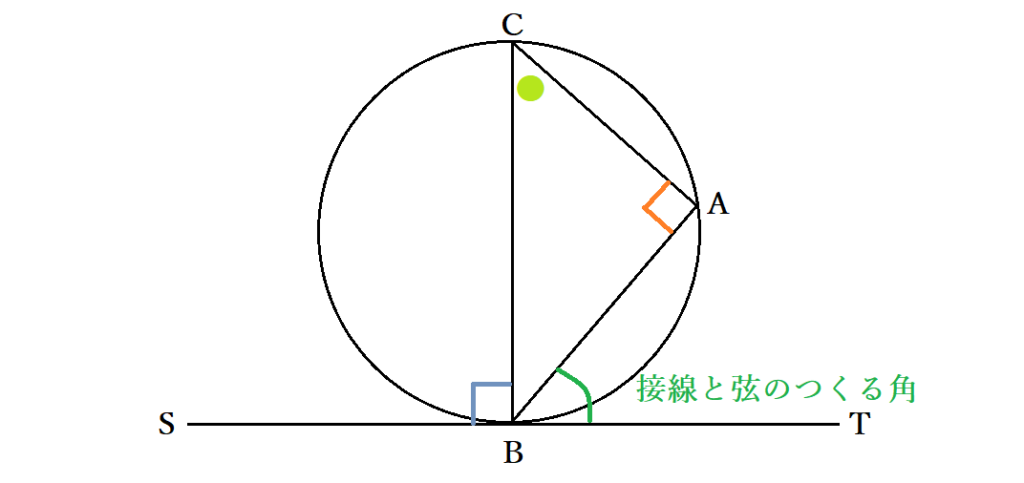
円に内接する三角形が直角の場合、円の接線が90度であることから ∠SBC=∠BAC=90度となります。 三角形の内角の和が180度・直線をなす角度が180°であることから他の部分を除いて、∠TBA=∠BCAです。
●接弦定理の証明:鈍角の場合
円の中心Oおよび接点Bを通る直線を引き、B以外の円との交点をDとおきます。ここで、DBは円の中心Oを通っているので、円の直径ですから、∠BAD=90度です。∠CAD=▲とおくと円周角の定理より弦が共通している円周角の大きさは等しいので、 ∠CAD =∠CBD= ▲ となります。
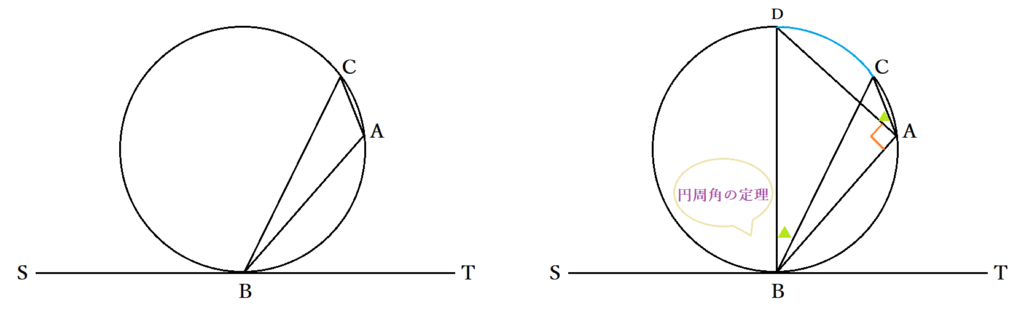
他方、BDは円の直径で接線と90度に交わることから、∠SBD=90°が成り立ち、∠SBC=∠SBD+∠CBD=90°+▲です。∠BAC=∠BAD+∠CAD= 90°+▲より、∠SBC=∠BACだとわかりました。三角形の和と直線の角度が180度であることから∠TBA=∠BCAも成立します。
◎円周角と接線を利用、接線と弦の作る角の問題
接弦定理の問題で高校ではどのようなものがあるのかも例題を通してご紹介しましょう。証明のときと同様に、円周角と接線を利用して問題を解くことに変わりはありません(以下で登場する数字はいずれも角度です)。
①
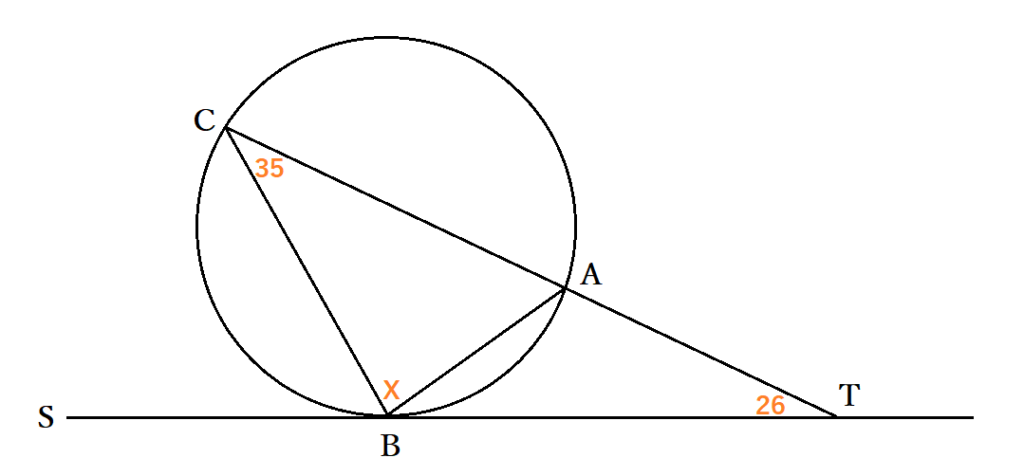
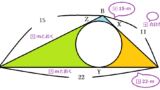
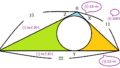
接弦定理の問題が高校の数学で出てくる場合には、少し捻りが加えられていることもあります。ただ、円の外側に出ている三角形を無視すると、これまで見ていた形です。三角形ABCにおいて接弦定理より∠TBA=∠BCA=35°が成り立ちます。次に、△ABTにおいて三角形の外角の性質より∠BAC=∠TBA+∠ATB=35+26=61°です。最後に、△ABCで三角形の内角の和が180度であることから、∠ABC=180-∠BAC-∠BCA=84°となり、X=84だとわかりました。
②円に内接する四角形でも接弦定理が使えることもあります。たとえばこのような問題だったときはどのように解答しますか?
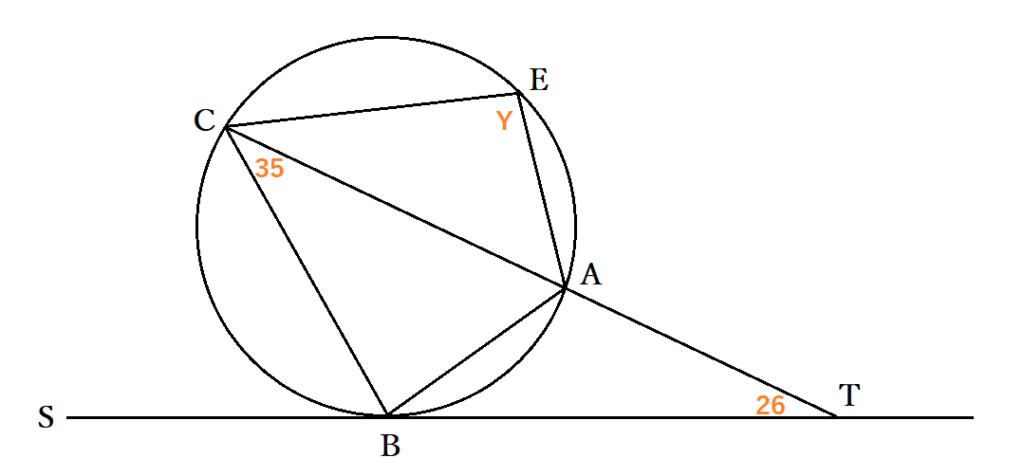
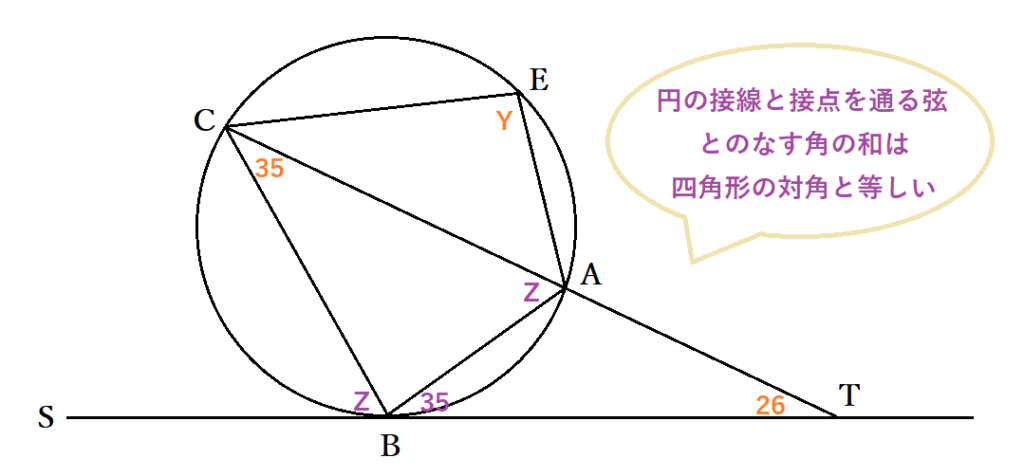
①と同じように解いてもできますが、ここでは少し違う考え方をしてみましょう。∠BAC=Zとおくと、接弦定理より∠SBC=∠BAC=Z・∠TBA=∠BAC=35°です。また、円に内接する四角形の性質より∠ABC=180-∠AEC=180-Yですが、直線STにおいて∠SBC+∠ABC+∠TBA=180°も成り立ちます。つまり、Z+180-Y+35=180より、Y=Z+35です。∠BAC=∠TBA+∠ATB=35+26=61のため、Y=96だとわかりました。
◎接弦定理の逆、証明はどのようにする?
接弦定理の逆とは、三角形ABCと直線STが点Bで交わっていて、SとAが直線BCに対して・ TとCが直線BAに対して違う側にあるとき、∠SBC=∠BAC・∠TBA=∠BCAが成り立つならば直線STが三角形ABCの外接円と接することです。接弦定理の逆の証明は、接弦定理を利用して接線に一致することを証明する方法がよく用いられています。
●接弦定理を利用して接線に一致することを証明する
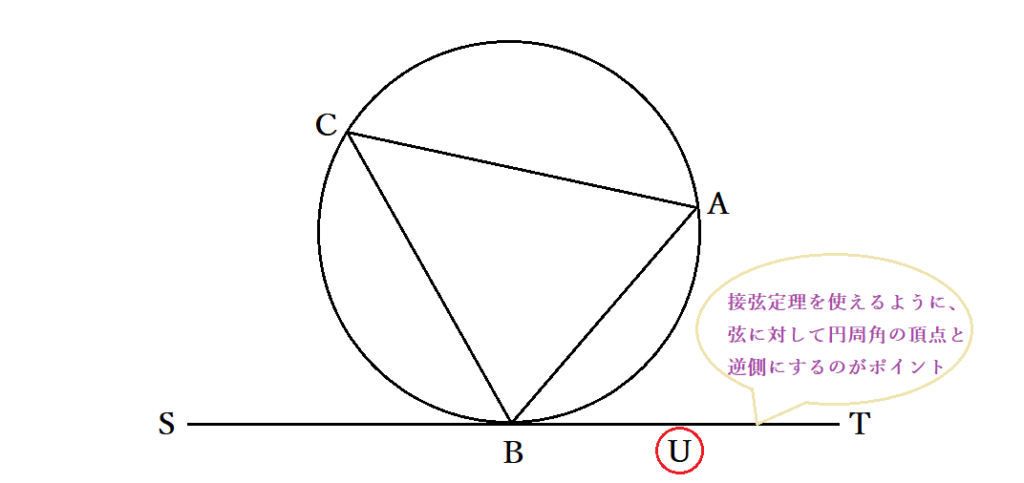
三角形ABCの外接円に関して、Bにおける接線を引き、ABに対してCと違う側にある点をUとおきます。このとき接弦定理より∠UBA=∠BCAです。一方で、仮定より∠TBA=∠BCAなので、∠TBA=∠UBAが成り立ちます。ここで、UとTはともに直線BAに対してCとは違う側にあるとしていたため、UとTが同一直線上にあり、直線STが接線に一致すると示せました。
ただ、接弦定理が成り立っていることを前提に逆を示すのはすっきりしない方もいらっしゃるかもしれません。そこで、接弦定理を使わずに接弦定理の逆が成立することを証明してみましょう。
●外接円を作図し、その接線が90度で交わることを示す
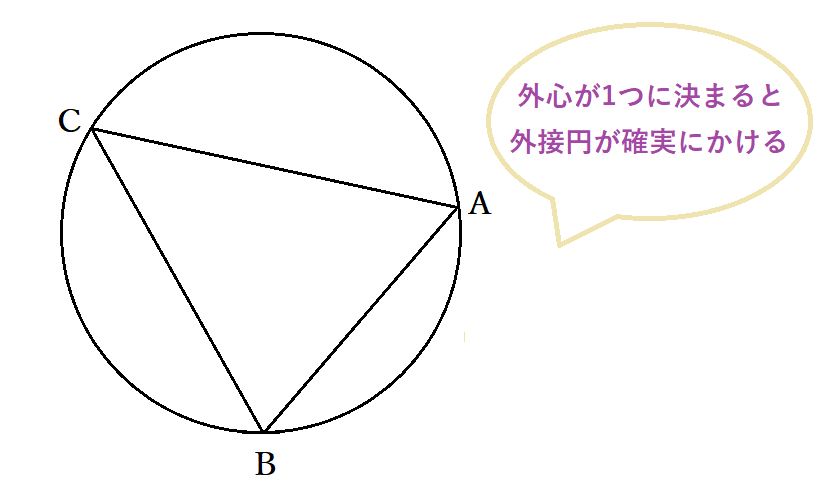
まず、三角形ABCに外接する円を考えます。三角形の外接円の作図は、外心(各辺の垂直二等分線の交点)をとり、外心を中心・外心と頂点を半径とする円を描くことで可能です。三角形の各辺はいずれも1点のみでお互いと交わるので平行・一致いずれでもなく、垂直二等分線同士も 平行・一致いずれでもないので1点で交わることから、外心も1通りに決まります。
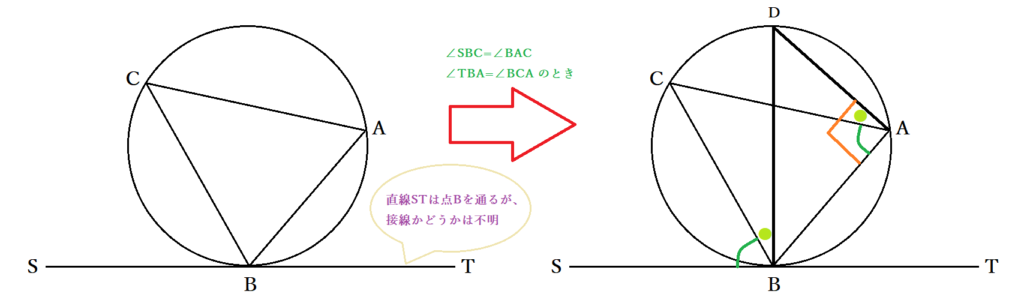
ここからは、三角形・外接円に対して直線STが接線であることを証明しましょう。直線と三角形の交点であるBから外接円の中心を通る線を引き、円周上の逆側の交点をDとします。このとき、BDは円の直径ですから∠BAD=90度で、円周角の定理より∠CBD=∠CADです。仮定より∠SBC=∠BACですから、以上の等式を合わせて、∠SBD=∠SBC+∠CBD=∠BAC+∠CAD=∠BAD=90°が成り立ちます。したがって、直線STは外接円の直径に垂直であることから、 直線STが三角形ABCの外接円と接することが示せました。
◎ 接弦定理の証明で用いた、 円の接線が90° であることの証明
接弦定理の証明では、円の接線が90°であることを利用しています。当たり前であるかのように使っている内容ですが、本当に必ず成り立つのかが気になるかもしれません。円の接線が90°で交わる原理や3つの証明方法などをこちらの記事で触れていますので、あわせて参考にしていただけますと幸いです。
◎接弦定理を利用した応用問題・証明
◎まとめ
今回は、接弦定理および接弦定理の逆の証明などをご紹介しました。証明は、円周角の性質や接線が円の直径と直交することなどを利用します。逆の流れや覚え方もあわせて理解しておくとスムーズに問題も解けるでしょう。最後までお読みいただきありがとうございました。