円の接線の性質や公式は知っていると便利なものが多いです。長さや角度の問題でスムーズに解答できるようにするためにも、公式やその原理を知っておきたいですよね。今回は、円の接線の性質である、円外の点pを通る円oの接線の長さが2本とも等しいことの証明とよくある問題の例をご紹介します。
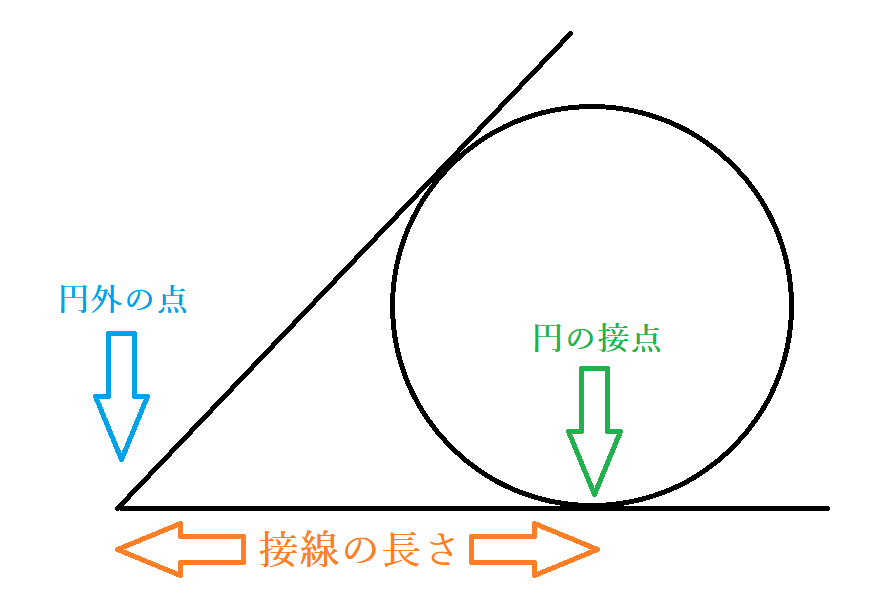
◎円の接線の性質で便利な公式『円の外部の点から引いた2本の接線の長さは等しい』
円の外部の点から円に引ける接線は2本あり、接線の長さとはその点と接点との距離です。円の接線の性質で便利な中学数学の公式として、『円の外部にある1点から引いた2本の接線の長さは等しい』があります。
◎円の接線の公式『円の外部の点pを通る円oの接線の長さが等しい』ことの証明
円の中心をO・円の外部の点をPとして、2本の接線と円との交点つまり接点をT・Hとおきます。ここでは、2本の接線は異なるものですから、TとHは円周上の別の点です。
三角形TPOとHPOにおいて、POは共通・TとHは円周上にあることからOT=OH(=半径)が成り立ちます。また、直線PTとPHは円の外部の点から引いた2本の接線ですから、円とは垂直に交わり、∠PTO=∠PHO=90度です。したがって、三角形TPOとHPOは斜辺と他の1辺がそれぞれ等しい直角三角形で合同関係が成り立ちます。
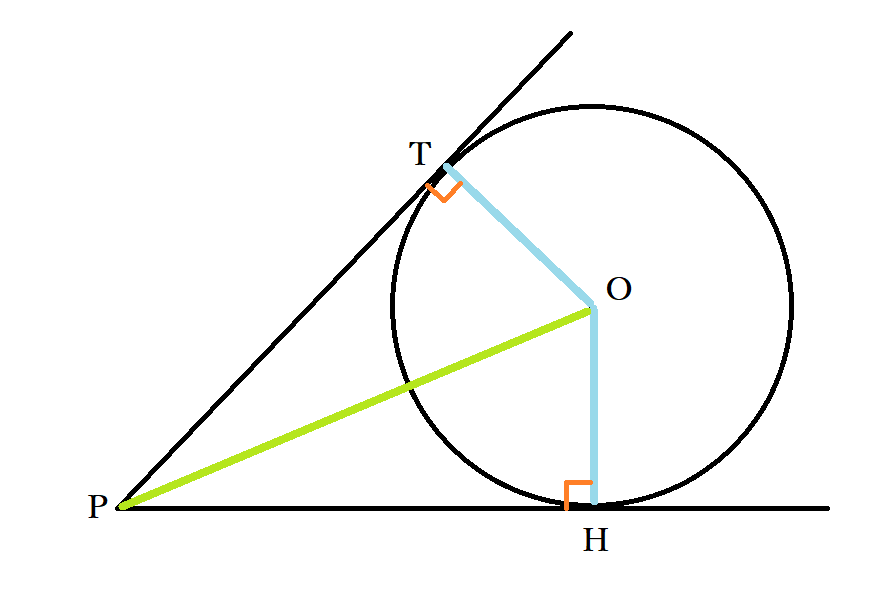
合同な三角形は対応する角度の大きさや辺の長さが等しいですから、PT=PHで題意である「円の外部の点pを通る円oの接線の長さが等しい」ことが示せました。また、∠TPO=∠HPOが成り立つので、円の中心と外部の点を結んだ直線は2本の接線の内角二等分線であることもわかります。
なおこの証明では、円と接線が90度で交わることを利用しました。円と直線がなす角がなぜ90度になるのかに関しては、以下の記事で3種類の証明をご紹介していますので、参考にしていただけますと幸いです。
◎接弦定理を使った、円外の点から引いた接線の長さが等しいことの証明
円と直線が接する際に成り立つ、接弦定理を利用しても、円の外部の点から引いた2本の接線の長さは等しいことの証明ができます。先ほどと同様に、円の外部の点をP・2本の接線と円との接点をT・Hとおきました。2本の接線は異なるものですから、TとHは円周上の別の点です。
ここでT・Hとは異なる円周上の点をSとして、三角形THSを作ります。
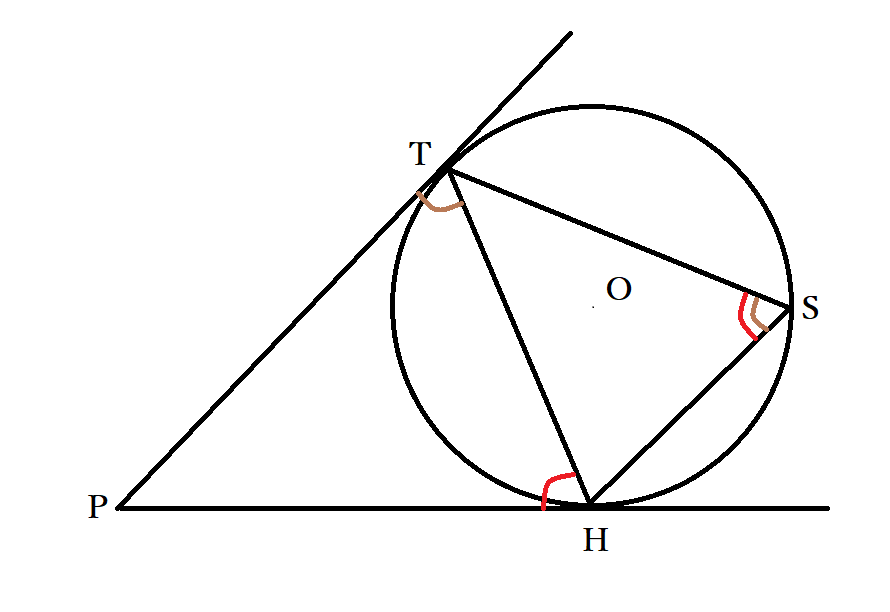
△THSは円に内接し、その円の接線がPT・HTであることから接弦定理より、∠PHT=∠HST・∠PTH=∠TSHです。よって、∠PHT=∠PTHで三角形PTHは二等辺三角形なので、PT=PHが成り立ち、円外の点から引いた2本の接線の長さは等しいことが示せました。
接弦定理がなぜ成立するのかはこちらの記事で詳しく触れていますので、参考にしていただけますと幸いです。
◎円と接線の性質を利用した長さの例題、内接円の半径の求め方も
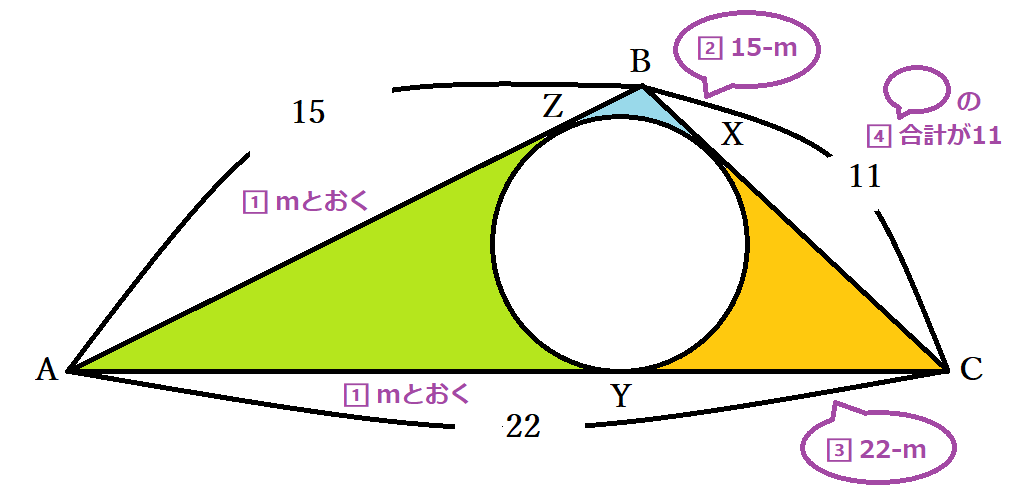
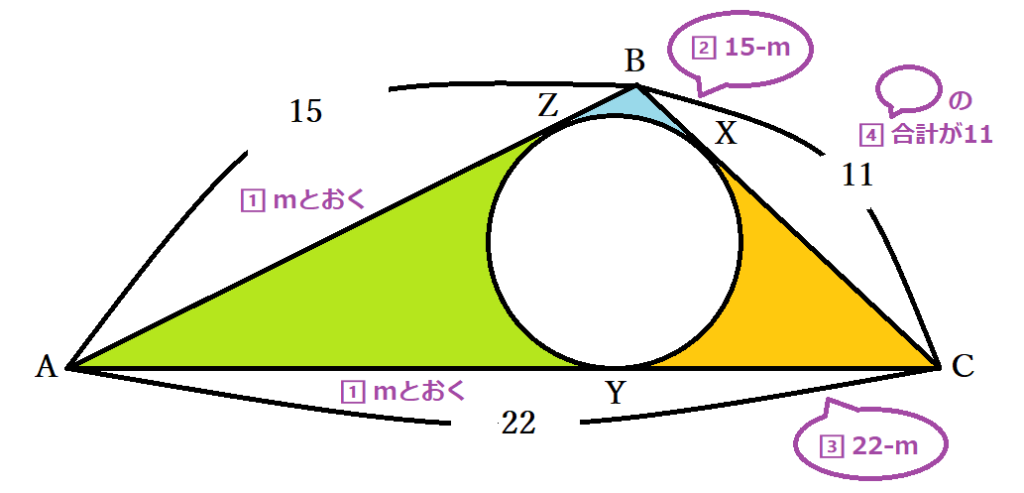
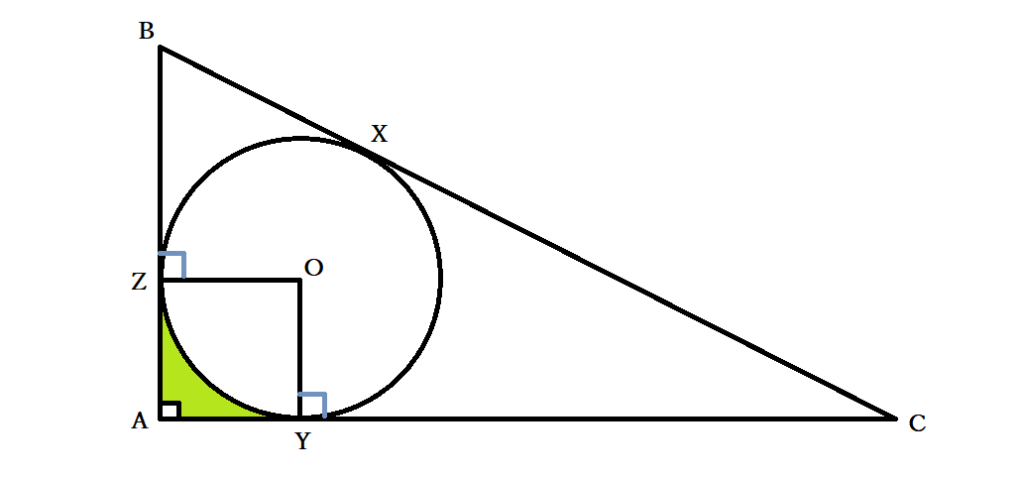
円と接線の性質『円の外部の点から引いた2本の接線の長さが等しい』ことは、内接円が絡んだ問題で長さを求める場合に便利です。たとえば、AB=15・BC=11・CA=22の三角形ABCがあり、内接する円が描かれていたとします。BC・CA・AB上での円と三角形の接点をそれぞれX・Y・Zとおいてみましょう。円の外部の点から引いた2本の接線の長さが等しいことから、AY=AZ=mとおくと、BX=BZ=AB-AZ=15-m・CX=CY=AC-AY=22-mと表せます。BC=11ですから、BC=BX+CX=15-m+22-m=11つまり37-2m=11より、AY=AZ=m=13・ BX=BZ=2・CX=CY=9だと求められました。
円が内接している三角形の1つの角が90度つまり直角三角形のときには、円の外部の点から引いた2本の接線の長さが等しいことを利用して円の半径を求められます。たとえば、先ほどの例で∠A=90度だったとすると、YとZが円と三角形の接点であることから角度は∠AZO=AYO=90度で、四角形OZAYは全ての角が90度です。さらに、AZ=AYと隣り合う2辺が等しいので、 四角形OZAYは正方形だとわかり、先ほどの方法でAZとAYが求まると半径も求められます。
◎まとめ
今回は、円の外部の点pを通る円oの接線の長さが等しいことの証明とよくある練習問題をご紹介しました。証明方法には、三角形の合同のほか、接弦定理を利用するものがあります。特に長さや角度を求める際に利用できる性質ですから、円と直線の問題が出てきたときには使えるかを試してみると良いでしょう。最後までお読みいただきありがとうございました。