立方体の展開図が何通りあるのかが気になるかもしれません。小学校や中学校の空間図形にとどまらず、TGWEBなどの適性検査でも図形の展開図の問題はありますから、立方体の展開図の数を把握しておきたいですよね。正六面体の展開図はルールを決めて場合分けをしたりサイコロの展開図が何通りあるのかで置き換えたりするのがおすすめです。今回は、立方体の展開図が何種類あるのかを考える方法と、サイコロなどの展開図の問題が適性検査などでどのように出るのかをご紹介します。
◎立方体の展開図は何通り?
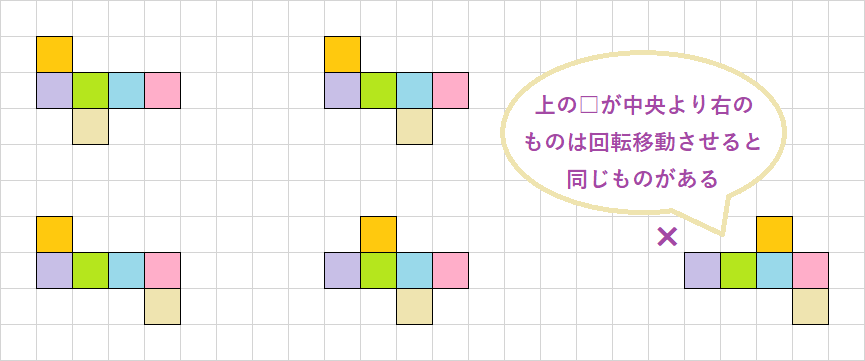
立方体の展開図の数は全部で11種類あります。それほど多くはない理由は、回転・対称移動によって重なるものがあるからです。たとえば、以下の図形はすべて同じものだとわかりますか?
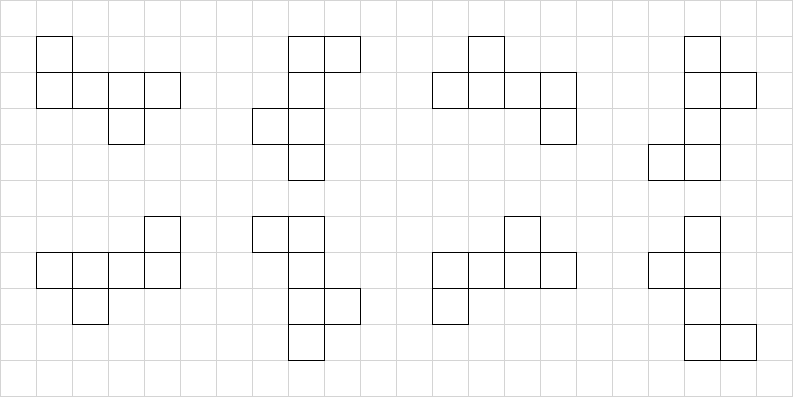
上側に並んでいる4種類の図形は、四つの面が連続し、上下に1つずつ面が接している一番左の図形を90度ずつ回転させたものです。また、下側に並んでいる4つの図形は、上側の四つの左右を逆にして配置しています。このように、回転させたり対称移動させたりすることで一致する展開図もあるため、注意しなければいけません。立方体の展開図が何通りあるかを考える際には、特定の面を固定させる必要があります。

◎正六面体/立方体の展開図の数が何種類あるかの考え方のポイント
正六面体の展開図の種類を考える際には、とりあえず6つ並べてみて組み立てられそうかを調べるのは大変かもしれません。適性考査などで展開図の問題が出てきた時には、6つの正方形が何個連続で同じ方向に並んでいるかによって場合分けするのがおすすめです。
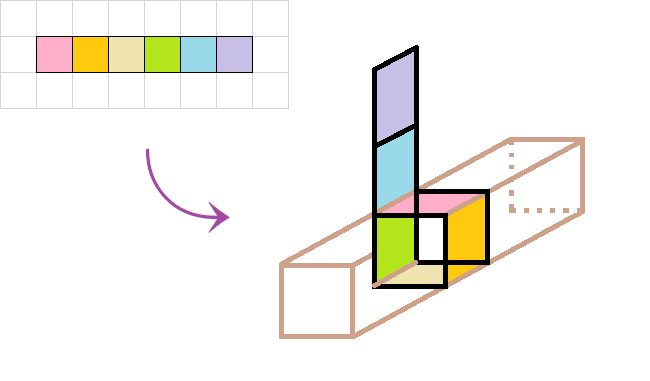
試しに、6つの面全てを同じ方向に並べようとするとうまくいきません。なぜなら、組み立てたときに、一番左の面を上にすると2番目以降右⇒下⇒左となり左から5番目の面が上に来て一致してしまうからです。つまり、5つ以上連続すると重なる部分が出てくるので、面が同じ方向に連続するのは最大で4つまでだとわかります。
◎サイコロの展開図で種類分け:立方体の展開図が11種類である理由と一覧
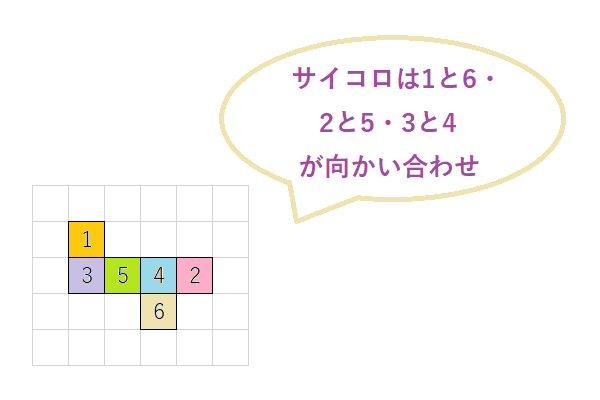
面が同じ方向に連続するのは4つまでのため、連続して並ぶ面が2・3・4つの場合それぞれにわけて、展開図を考えていきましょう。下の図のようなサイコロとしてそれぞれの場合で展開図が何個あるのかを考えていくとわかりやすいかもしれません。ただし、実際には区別がなく全く同じ形(正方形)のため、単に数字が入れ替わっているだけのものは同一の展開図である点に注意です。
●連続して並ぶものが4つの場合
連続して並ぶ4つの面を③⑤④②の場合のみを考えます。このとき、①と⑥の面は互いに接することがないように位置するので、③⑤④②に対して反対側です。①と⑥の配置は、お互いに同じ面に対して向かい合っている場合と違う面に接している場合があります。同じ面に接しているのは、一番端か内側かの2通りです。たとえば、②の面で向かい合っているものは回転させると③で向かい合っているのと同じ図形になります。
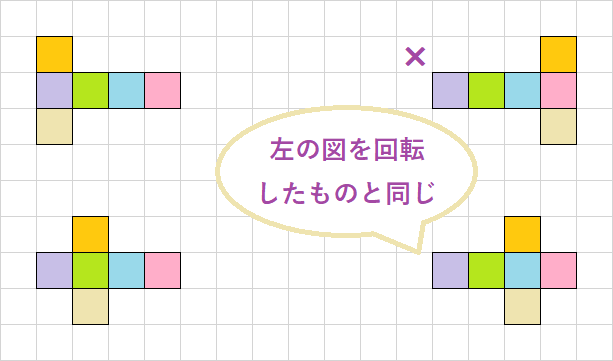
違う面に接しているのは、③⑤の場合・③④の場合・③②の場合・⑤④の場合の4通りです。端同士・内側同士・片方が端でもう片方が内側のどちらかに位置しています。⑤②の場合は回転移動させると③④の場合に一致し、上にある橙色の面が②に面する場合には、左右対称で一致するものがあるのでカウントしません。
●連続して並ぶものが3つの場合
ここまでで、サイコロの展開図11種類のうち6個が出てきました。同じようにいくつかの面を固定して考えていきます。ただし、今回は並べ方によっては別の場所にも3つ連続ができたり、NG例として縦向きに4面連続があったりするので注意しましょう。
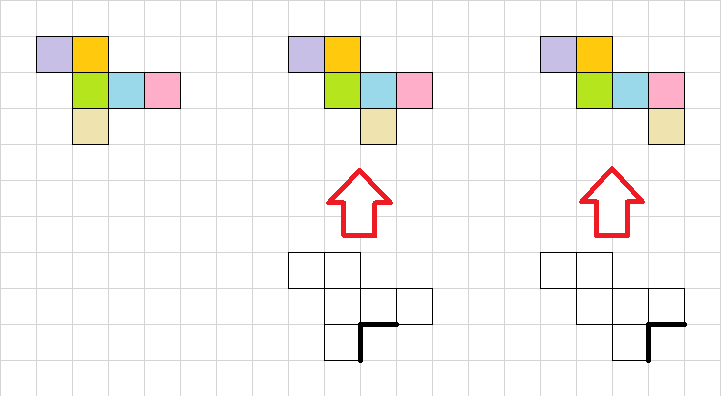
ここでは、⑤④②の面を固定して①②③の面を動かしていきます。先ほど、4面連続+上下に向かい合う形の立方体の展開図がありましたが、このうち内側で向かい合っているものに注目しましょう。③に該当する外側にはみ出した部分は、実際に立方体を組み立てると①の面にも接しているので、黒く塗った辺同士をくっ付けるようにして移動しても問題なく組み立てられます。よって、これが連続して並ぶ面が3つのもののうちの1つ目の展開図です。

さらに、先ほどと同様に、下側⑥の面をスライドさせられるので、3面に対して上側に横2面・下側に1面が向かい合うもののほかにも、1つずれているもの、2つずれているものも立方体の展開図として成立します。一方で、横2面をずらすと組み立てた際に被る箇所が生じ、縦向きに並べても回転させると同じ展開図になってしまってうまくいきません。
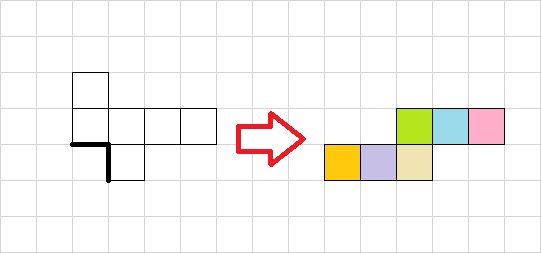
立方体の展開図のうち残りの2種類は、非常に特殊な形をしています。先ほどから①と⑥の面は連続する面に対して逆側にくるように考えてきましたが、例外が存在するのです。そのうちの1つが、3つ連続したものの端からさらに3つの四角が連続しています。実感がわかない場合には、別の展開図のうち、2面を動かすと想像しやすいかもしれません。
●連続して並ぶものが2つの場合
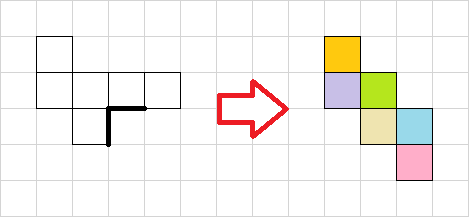
立方体の展開図のうち、連続して並ぶ面が2つのものは1通りのみが考えられ、下の図のようにジグザグに並んでいます。イメージし辛い場合には、先ほどの4面が並んでいる展開図から連想すると良いでしょう。使うのは、同じく片方が端でもう片方が内側の逆の面に位置している展開図です。右側の2つを黒い点を中心に回転させると、ジグザグに並んだ展開図に変わります。
◎サイコロの展開図に関してどのような問題が適性検査で出題されるのか?
TGWEBなど適性検査で出てくる図形の展開図の問題は主に2種類が考えられます。1つ目は、展開図としてふさわしいものがどれなのかを選ぶ問題です。サイコロの展開図は11種類ですから、形を覚えておけば適性検査でも難なく解けるかもしれません。万一忘れた場合には組み立てることになりますが、上記で説明した方法で考えると就職活動の緊張した場面で出てきても混乱しないでしょう。
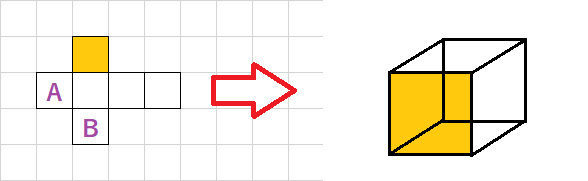
展開図の問題として適性検査で出てきやすいもう一つのパターンが、展開図に文字や記号が書かれていて、組み立てたときに向きを問うものです。この場合は、1マスずらすと90度回転することに注意しましょう。たとえば、AとBが描かれている場合、組み立てるとBは2回90°回転するため、ちょうど逆向きに見えます。頭の中で想像できれば問題ないですが、難しいのであれば、対応する辺を書き出して動かしていくのがおすすめです。
◎まとめ
今回は、立方体の展開図が何種類あるのかについて、考え方などをご紹介しました。サイコロの展開図として考えて何通りあるのかを導き出すなど工夫するのがおすすめです。TGWEBなど適性検査でも展開図の問題は出てくる可能性がありますので、何度か試して素早く書き出せる方法を見つけると良いでしょう。最後までお読みいただきありがとうございました。
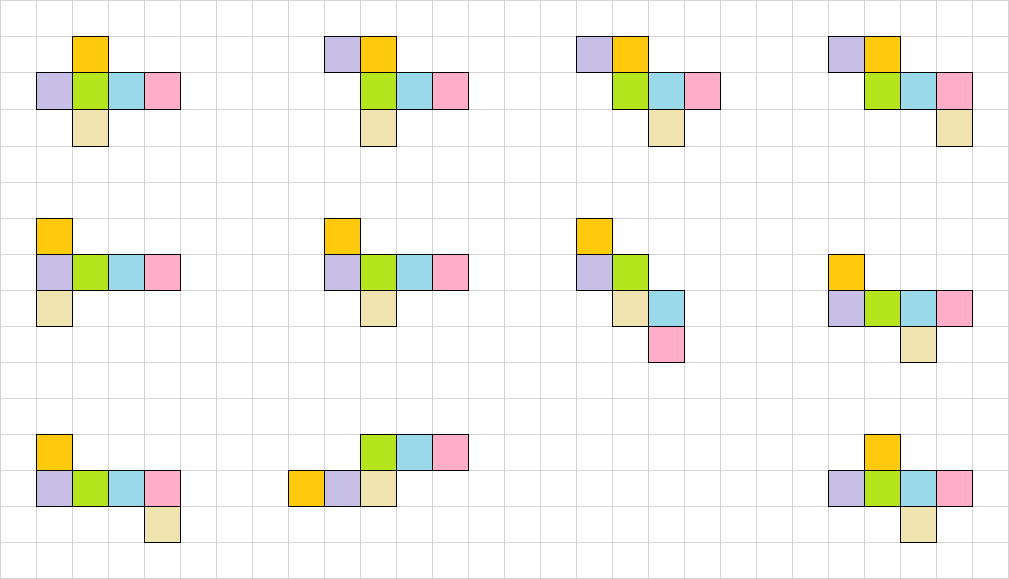


コメント