共通テストの各科目の難易度に関連して、平均点も気になるかもしれません。特に英語や国語、数学といった主要科目は受験者数も多く、平均点の推移を見ることで試験全体の難易度を把握しやすいですよね。共通テストやセンター試験では平均点推移として5教科7科目といった枠組みが用いられることがありますが、そもそもの定義や計算のやり方が時期によって異なる点を押さえておくことが重要です。今回は、共通テストの平均点の変遷を英語や国語といった科目別に触れ、合計を見る際の注意点などとともにご紹介します。
◎共通テストの平均点(英語・国語・数学)教科別に
共通テスト(2021~)の平均点として、まずは受験者数が多い主要3教科を見ていきましょう。公式発表の確定値を基にしたグラフであり、全体の難易度を左右しやすく、毎年話題になりやすい分野です。
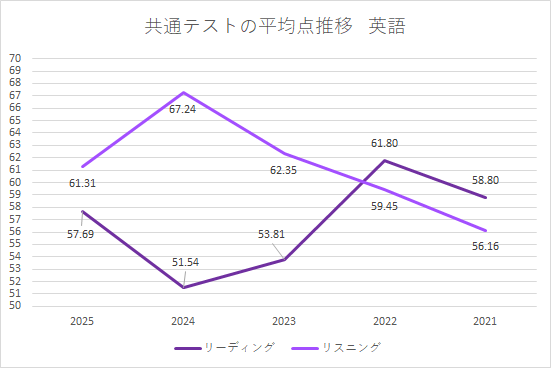
共通テストの平均点のうち英語は、リーディングとリスニングの2種類があります(それぞれ100点満点)。年度による差はありますが、極端に低くなりにくく、過去5年はいずれも50.60点台に収まっているのが特徴です。
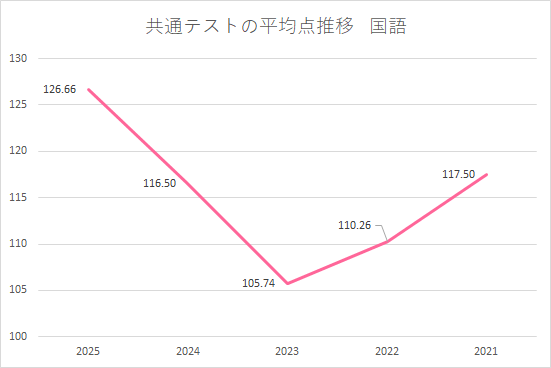
共通テストの平均点のうち国語は、200点満点で表示しています。当初検討されていた記述は現時点で導入されておらず、10分長い90分になりました。過去5年は105.74~126.66点の範囲で推移しており、設問形式や文章の読みやすさによって平均点が動きやすい教科です。
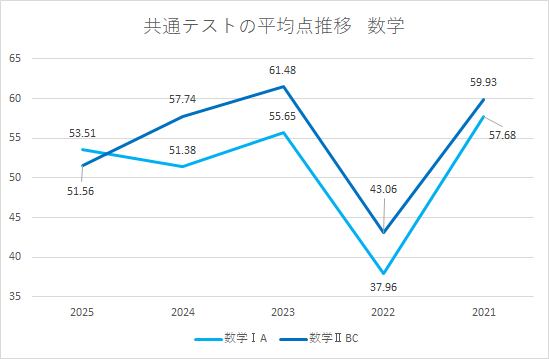
数学は、共通テストの中でも平均点の振れ幅が目立ちます。得点調整で話題となった2023は2日目の試験の慰めになったものの、その前年の共通テストは数学の平均点がIA37.96点で過去最低・数学ⅡBも43.06点を記録しました。合計でいえばセンター試験時代を含めても最低記録であり、共通テストの特徴である知識だけでなく思考力を問う問題が増加したことが原因だと考えられます。
◎大学入学共通テストの平均点の推移を見る際の注意点
共通テストにおいては、「合計点」や「5教科7科目の平均点」といった表現を目にすることがあるかもしれません。しかし、主催者の大学入試センターは合計点の平均を公表しておらず、発表しているのはあくまでも各教科・科目ごとの平均点のみです。つまり、合計点や文系・理系別の平均点は、何らかの計算や仮定を置いた推定値になります。この点を理解せずに数値だけを見ると、年ごとの比較を誤って解釈してしまうかもしれません。大学入学共通テストの平均点の推移を見る際には、これらの合計点がどのような計算で求められているのかまで見ておくことが重要です。
また、共通テストやセンター試験は科目や配点が頻繁に代わっており、平均点の推移を総合でみる際には単純な比較ができない点も押さえておく必要があります。たとえば過去15年では、2015年に課程が変わって理科基礎が登場したほか、2021年の共通テストからは英語の200点満点の内訳が変化しました。さらに、2025年からの新課程では社会の科目の構成に変更があり、さらに情報Ⅰが追加されたことで、5教科7科目という考え方がそのままでは使えなくなりました。比較している対象が同じものか、代替とみなせるものであるかなどはしっかりと把握して分析していくことが必要です。
◎共通テストの平均点の推移【合計・理系・文系】
共通テストの平均点の推移を、理系や文系の5教科7科目といった合計でみていきましょう。大学入学共通テストの平均点の推移は、この記事においては以下の方法で算出しています。
🔴3教科合計=国語(200点満点)+数学ⅠA(100点満点)+数学ⅡBC(100点満点)+英語(200点満点)
※共通テスト(2021~)はリーディング100点満点+リスニング100点満点
センター試験(~2020)は筆記200点満点とリスニング50点満点を合計して0.8倍に圧縮
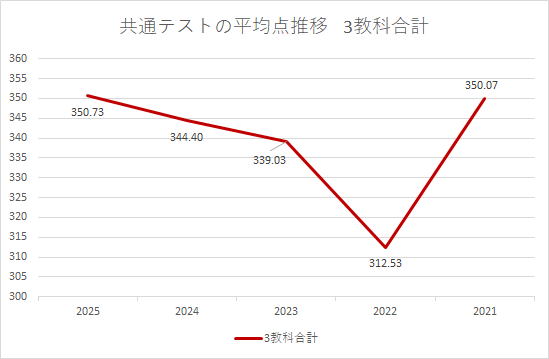
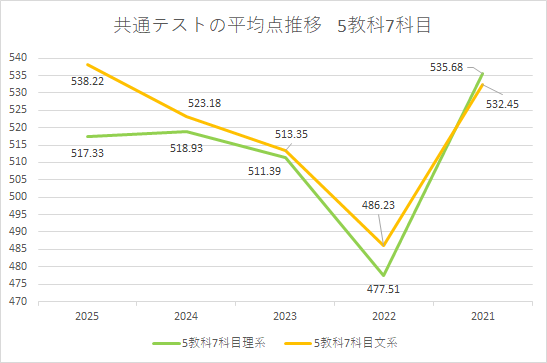
共通テストの平均点の推移を3教科の合計で見た場合、2022年が群を抜いて低いことがわかります。先述の通り、数学の平均点が全体的に低かったことが要因です。共通テストの平均点の推移としては、2023以降は数点ずつ上がってきており、落ち着いた動きを見せています。
次に、理科社会を入れた点数で共通テストの平均点の推移を見てみましょう。
🔴5教科7科目理系=3教科合計+(理科の各平均点×受験者数)の合計÷受験者数合計×2+(社会の各平均点×受験者数)の合計÷受験者数合計
🔴5教科7科目文系=3教科合計+(理科基礎の各平均点×受験者数)の合計÷受験者数合計×2+(社会の各平均点×受験者数)の合計÷受験者数合計×2
理系は理科2科目+社会1科目・文系は社会2科目+理科基礎2科目を受験すると仮定したものです。理科と社会は、それぞれの総合計点を算出することで「任意の1科目を受験したときの”期待平均点”」(どの科目を選んでも平均的にはこの点数になると考えられる目安)として算出しています。また、理科基礎科目は50点満点を2科目選択、理系の理科も2科目・文系の社会も2科目なので、それぞれ×2です。
同様に2022年は共通テストの中では最も低く、2023以降が徐々に上がるのも3教科合計と同じですが、興味深いのは2025年の理系と文系の点差が広がっていることでしょう。理系はむしろ合計値ベースでは下がっており、これは2025年の理科が化学・生物をはじめとして点数が伸び悩んだ科目が多かったことが原因として挙げられます。
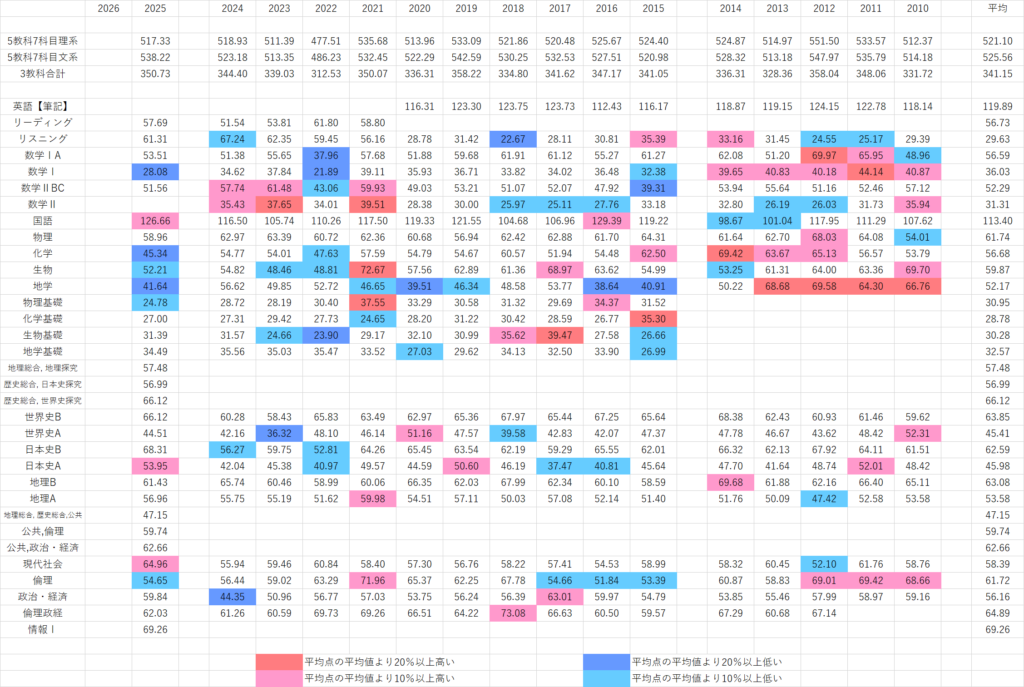
◎センター試験の平均点推移(2020までの総合/5教科7科目など)と共通テストとの違い
共通テストの平均点を考える際に、比較対象として挙がるのがセンター試験です。センター試験時代は、特に5教科7科目の枠組みで総合平均点が語られることが多く、現在でもこの形式で語られることは珍しくありません。センター試験は長期間にわたって実施されていたため平均点の推移を年単位で追いやすく、難易度の変化も把握しやすい試験でした。センター試験の平均点推移について2020までの記録を5教科7科目などでみてみましょう。英語リーディング(筆記)は平均値から10%以上振れた年がないほど安定している一方で、他の科目は年によって大きく上がったり下がってりしていることがわかります。
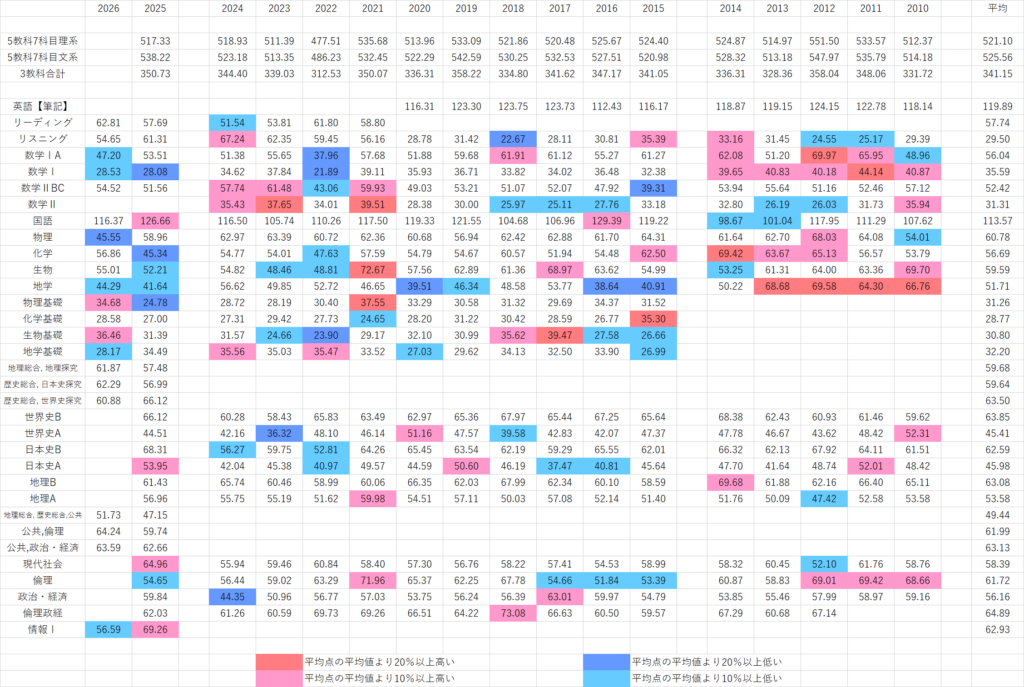
[2026年2月6日追記]
共通テスト2026の平均点(最終発表)と比較すると、物理は45.55点と前年から10点以上下がりセンター試験時代を含めても過去最低水準となりました。また、数学IAは47.20点と久々に5割を下回り、2022年に次ぐ水準です。リスニングは54.65点(-6.66)、国語は116.37点(-10.29)と、点数ベースでは前年より下がり、一方で化学は56.86点(+11.52)と前年からは10点上がっていますが、センター試験時代と比較すると平年並みの水準に落ち着いています。
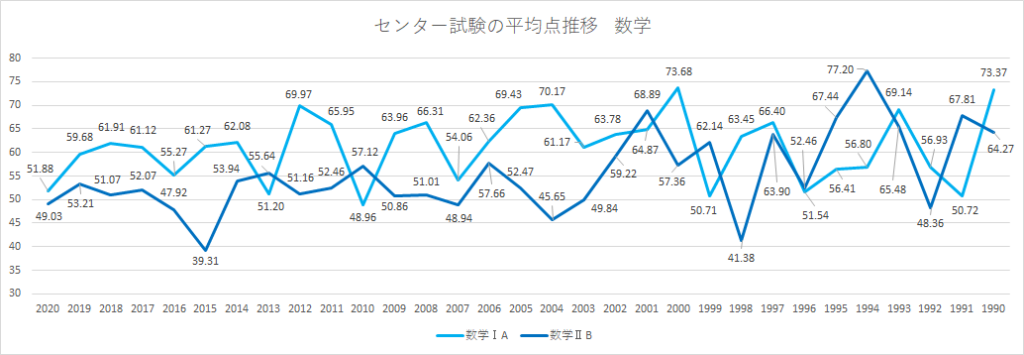
●センター試験の数学の平均点推移:平均点が最低から大幅反発した1993など
センター試験の中でも、数学は平均点推移の激しかった科目です。数学ⅠA・ⅡBともに、年度によって平均点が大きく変動し、難易度の象徴として語られる年がいくつもあります。センター試験が始まって間もない頃の1992年は前年から19.45点と平均点が急低下し、1993年には大幅に反発して17.12点の上昇がありました。数学ⅡBは1997~1999年も63.90点→41.38点→62.14点と20点以上の差があり、00年代以降こそまだ幅は小さいですが、10点近く変わることも珍しくありません。センター試験の数学の平均点が最低だった年として知られるのが2015年です。この年は前年の53.94点から39.31点と14.63点下がっています。また、数学ⅠAは前年から15点平均点を下げ、翌年は17点上げた2010年が唯一の5割を切った年でした。共通テストでは数学ⅠAの方が低いことが多いですが、センター試験時代は割と大差で数学ⅡBを上回っているのがわかります。
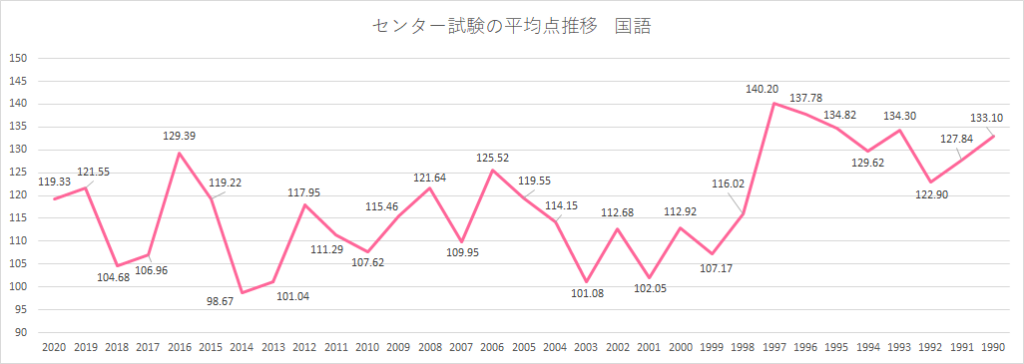
●センター試験の国語の平均点推移:平均点が大幅に低下した2014
センター試験の国語の平均点推移で特に有名なのが、2014・2013年です。この2年は国語の平均点が大幅に低下し、特に2014年は初めて平均点が5割を切りました。直前の2012年が117.95点で、この試験を中心に対策を進めていた受験生は本番になってレベル差に大きく苦戦しました。国語が苦手な筆者が地獄に落ちたのは言うまでもありません。数学ほどではないですが、年による変動が激しい科目ですから、過去問を使って演習する際には、どの程度の平均点であったかをしっかりと見てから目標の得点を定めるようにしましょう。
◎まとめ
今回は、共通テストやセンター試験の平均点について、教科別の推移や特徴を確認し、あわせて総合で見る際の注意点をご紹介しました。共通テストでは公式に発表されていない数値も多く、推定値を用いる場合には計算方法や前提条件を理解しておくことが重要です。また、センター試験との制度の違いを踏まえることで、平均点の変化をより正確に捉えられるようになります。今後の学習計画や過去問分析の参考として、感覚的な難しさに一喜一憂せず、推移や傾向を冷静に活用しましょう。最後までお読みいただきありがとうございました。
関連記事:平均点によって実施の有無が決まる、得点調整について
最新情報について




