2023年と同じカレンダーが過去のいつに該当するか、何年後にまた使えるのかが気になるかもしれません。2023年と同じ暦がいつなのかがわかると、曜日を特定するのも簡単にできますよね。同じ日が同じ曜日になるのは、何年ごとというある程度の法則性を持っているのが特徴です。今回は、今年と同じカレンダーが何年前・何年後に使えるのかに関して、曜日の周期や考え方をご紹介します。 (2022年版はこちら)
◎同じ日/同じ曜日になるのは何年ごと？カレンダーは何年周期なのかも
同じ日に同じ曜日になる状態が何年ごとに来るのかを考えるには、うるう年の規則性を押さえておく必要があります。うるう年とは、暦と太陽の動きが違うことで季節がずれるのを調整するために設定されている、366日という1年が通常より1日多い年のことです。現在のグレゴリオ暦では、うるう年は以下のようなルールがあります。2000年が閏年だったことで1901～2099の約200年は①の規則が当てはまるため、この記事を見ている皆さんのほとんどは「うるう年は4年に1回」と思っていても特に問題はありません。
曜日の1年ごとのずれは、365=7×52+1または366=7×52+2より、1日または2日です。余りが1日または2日とは、先の方にずれることになるため、例えばある年のある日が火曜日だった場合、その翌年の同じ日は水曜日または木曜日になります。毎年同じ曜日になる日というはなく、誕生日が毎年同じ曜日だということもありません。逆に言えば、毎年必ず曜日のずれはあり、何年かすると元に戻る周期もあると考えられます。そこで、カレンダーに置き換えて考えてみましょう。
●同じ日が同じ曜日になるのは何年ごとなのか？
1901年から2099年まではうるう年(1年が366日)になるのは4で割り切れる年です。4で割って余り1.2.3の場合はいずれも365日になります。カレンダーを何年周期で使い回しができるかについては、うるう年で設定されている2月29日があるため、2月までと3月以降で分けることが必要です。基準となる日の曜日をDとし、次の曜日をD+1・D+2…と表すものとしましょう。たとえば、Dが火曜日なら、D+1は水曜日・D+2は木曜日…D＋6は月曜日になります。
・1月と2月
余り0のうるう年の場合、2月29日がこの後あるため、翌年の同じ日までは366日です。そこで、曜日は1年後にはD⇒D+2になります。そこから3年間はうるう年ではなく、曜日は1つずつずれていくため、曜日の変化はD⇒D+2⇒D+3⇒D+4⇒D+5です。5年目はまた閏年で曜日が2つずれるため、D⇒D+2⇒D+3⇒D+4⇒D+5⇒D+7と変化して同じ曜日に戻ることがわかります。その年がうるう年であれば、5年後に同じ曜日になりました。
同様に、余り1/2/3の年はそれぞれ4年目/3年目/2年目にうるう年が来ることに注意すると以下のように曜日が移り変わります。(数字〇は曜日のずれの数)
余り0の年：D⇒②D+2⇒①D+3⇒①D+4⇒①D+5⇒②D+7
余り1の年：D⇒①D+1⇒①D+2⇒①D+3⇒②D+5⇒①D+6⇒①D+7
余り2の年：D⇒①D+1⇒①D+2⇒②D+4⇒①D+5⇒①D+6⇒①D+7
余り3の年：D⇒①D+1⇒②D+3⇒①D+4⇒①D+5⇒①D+6⇒②D+8⇒①D+9⇒①D+10⇒①D+11⇒②D+13⇒①D+14
余り3の年の場合はちょうど閏年のタイミングで同じ曜日を飛ばしてしまうため、次に曜日が同じ年が来るのは11年後です。したがって、1月1日から2月28日に関しては、カレンダーで同じ曜日になる周期が5年・6年・11年のいずれかとなります。
・3月以降
余り0の年は、既に2月29日は終了しており、1年後に366日経過するのは余り3の年であることに注意しましょう。
余り0の年：D⇒①D+1⇒①D+2⇒①D+3⇒②D+5⇒①D+6⇒①D+7
余り1の年：D⇒①D+1⇒①D+2⇒②D+4⇒①D+5⇒①D+6⇒①D+7
余り2の年：D⇒①D+1⇒②D+3⇒①D+4⇒①D+5⇒①D+6⇒②D+8⇒①D+9⇒①D+10⇒①D+11⇒②D+13⇒①D+14
余り3の年：D⇒②D+2⇒①D+3⇒①D+4⇒①D+5⇒②D+7
カレンダーで同じ曜日になる周期はやはり5年・6年・11年のいずれかです。
●カレンダーは何年周期なのか？
さて、この余り〇の年は、どこから始めても他の3つを経由することに気付かれている方もいらっしゃるかもしれません。たとえば、1月と2月の余り0の年だった場合は、5年後に同じ曜日になるので次は余り1の年の曜日の移り変わりが適用されます。そして6年後に同じ曜日になって次は余り3の年なので11年後に同じに、さらにそれは余り2の年ですから今度は6年後に同じ曜日になり、再び余り0の年に戻るのです。つまり、曜日は…⇒5年⇒6年⇒11年⇒6年⇒…の繰り返しで同じになることがわかります。これが28年の太陽周期とも言われる規則性であり、曜日の7とうるう年の周期4の最小公倍数とも同じです。
カレンダーの使い回しをどの頻度でできるかはもう一段階踏み込み必要があります。うるう年がある年とない年では2月までと3月以降の並びが変わるためです。28年間では7年がうるう年で21年が平年であり、閏年はそれぞれの曜日のカレンダーを1回ずつ・平年は3回ずつ使うことができます。
◎2023年と同じ曜日の年、過去にはいつがあった
ここまでの計算方法を踏まえて、2023年と同じ曜日の年が過去いつにあったのかを調べてみましょう。2023年と同じ暦を過去に向かって探す場合には、次の2つの方法が考えられます。
〇…⇒5年⇒6年⇒11年⇒6年⇒…の繰り返しを逆向きに調べる
先程の考察で、余り3の年になるのは余り1の年の6年後であることがわかりました。そこで、逆に6年前の2023-6=2017年が2023年と同じ曜日まわりだと計算できます。同じように…⇒5年⇒6年⇒11年⇒6年⇒…の繰り返しを逆向きにたどっていくのです。曜日が同じになる年は2月までは6年⇒5年⇒6年⇒11年・3月以降は6年⇒11年⇒6年⇒5年、と月によって異なる点には注意しましょう。
〇28の倍数で引き算をしてから、…⇒5年⇒6年⇒11年⇒6年⇒…の繰り返しで年数を出す
28年周期であることを利用し、一旦28年前・56年前・84年前と節目に戻ってから次に曜日が同じになる年を探します。2023は余り3ですから、繰り返しは2月までは11年⇒6年⇒5年⇒6年⇒…・3月以降は5年⇒6年⇒11年⇒6年⇒…の順番です。
どちらの計算方法でも当然ですが結果は同じで、2023年と同じ曜日まわりだったのは、1月と2月が2017年・2012年・2006年・1995年・1989年・1984年・1978年・1967年・1961年・1956年・1950年・1939年・1933年・1928年・1922年・1911年・1905年、3月以降は2017年・2006年・2000年・1995年・1989年・1978年・1972年・1967年・1961年・1950年・1944年・1939年・1933年・1922年・1916年・1911年・1905年だとわかりました。
●2023年と同じ曜日まわりが次に来るのは？
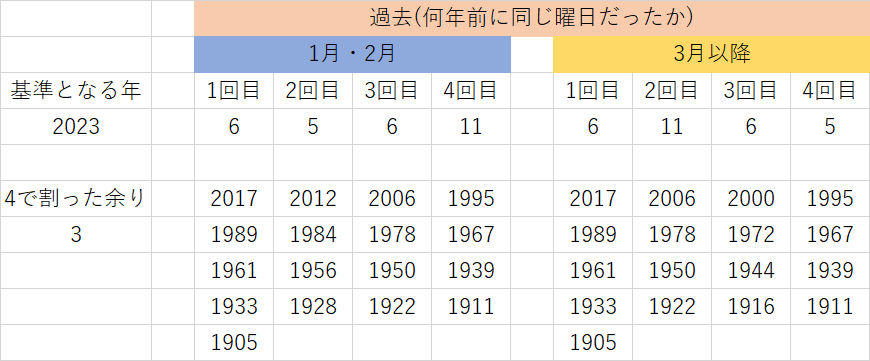
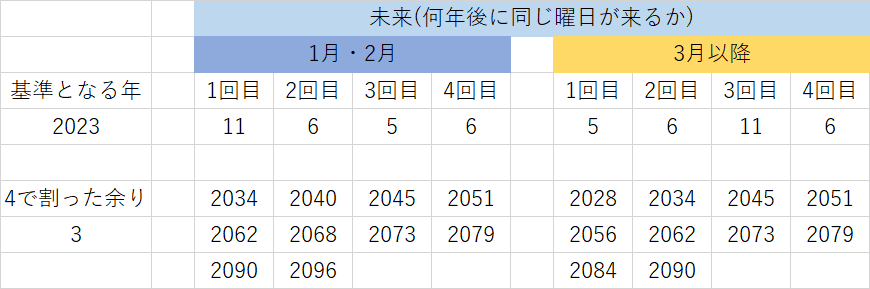
次に、2023年と同じ暦になる未来の年です。繰り返しは2月までは11年⇒6年⇒5年⇒6年⇒…・3月以降は5年⇒6年⇒11年⇒6年⇒…の順番になります。曜日が同じになる年を2023を基準に同様に計算すると、2月までは2034年・2040年・2045年・2051年・2062年・2068年・2073年・2079年・2090年・2096年、3月以降は2028年・2034年・2045年・2051年・2056年・2062年・2073年・2079年・2084年・2090年です。
◎2023年と同じカレンダーは過去にはいつがあった？
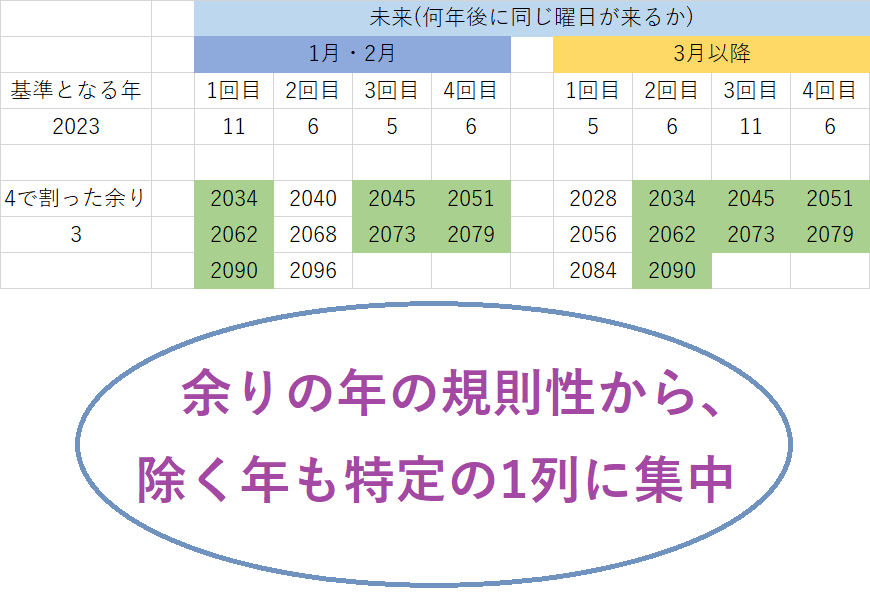
2023年と同じカレンダーが過去にはいつだったかを調べるには、同じ曜日の年の中で、1月2月も3月以降も該当しているものを選べるとスムーズです。先ほどの計算から、2017年・2006年・1995年・1989年・1978年・1967年・1961年・1950年・1939年・1933年・1922年・1911年・1905年が該当することがわかります。うるう年は1月2月と3月以降のどちらかはずれるので、4の倍数の年のみを除くと考えても良いでしょう。
●曜日が同じになる年 2023年以降はいつ？
同様に、2023年よりも後で同じカレンダーを使うことができるのは、2034年・2045年・2021年・2062年・2073年・2079年・2090年などです。28年周期で3回使えるということがここからもわかるでしょう。
さて、2100年を超える場合には、うるう年ではないため上記の計算方法が利用できない点に注意する必要があります。ちなみに、2099年は2026年と同様に1月1日が木曜日で始まる年のため、2100年は金曜日スタートです。2101年は土曜日・2102年は日曜日・2103年は月曜日・2104年は火曜日スタートと平年が続いたあと、2105年は木曜日と再び2日ずれが出てきます。100の倍数かつ400の倍数ではない年を超える場合は、一旦その周辺の曜日を特定し、リセットして考えると間違えづらいかもしれません。
◎まとめ
今回は、今年と同じカレンダーはいつ使えるのかに関して、同じ日が同じ曜日になるのはどれくらいの頻度なのかも含めてご紹介しました。曜日の1年ごとのずれが1日または2日のため、毎年同じ曜日になる日はありませんが、何年かすると元に戻る周期が決まっているのも特徴です。カレンダーを使い回しする場合には、うるう年と平年で周期が変わる場合がある点も押さえておくと良いでしょう。最後までお読みいただきありがとうございました。
昨年版はこちら⤵
コメント